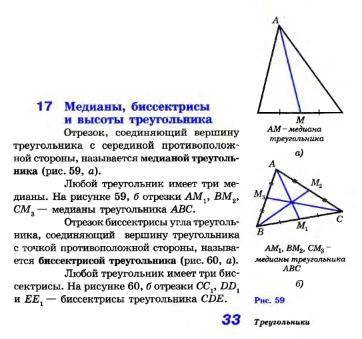
Медиана треугольника - отрезок, соединяющий вершину треугольника с серединой противоположной стороны. (рис, 59 а)
Биссектриса треугольника - отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. (рис. 60 а)
Высота треугольника - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. (рис. 61)
Любой треугольник имеет:
· три медианы (рис. 59 б)
· три биссектрисы (рис. 60 б)
· три высоты (рис. 62 а, б, в)
Свойства:
- в любом треугольнике медианы пересекаются в одной точке.
- в любом треугольнике биссектрисы пересекаются в одной точке.
- в любом треугольнике высоты или их продолжения пересекаются в одной точке.

ответ: √82 см
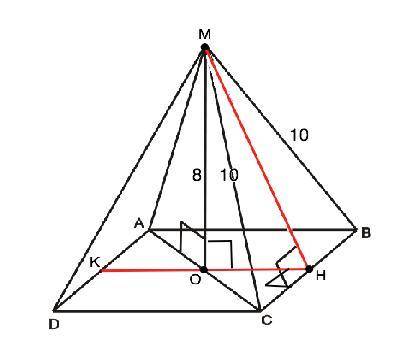
Объяснение: Вершина правильной четырехугольной пирамиды проецируется в центр основания - точку пересечения диагоналей квадрата. Пусть данная пирамида МАВСД, О - точка пересечения диагоналей основания. МО=8 - высота. МС=10 - боковое ребро, МН апофема ( высота боковой грани правильной пирамиды)
Из прямоугольного треугольника МОС по т.Пифагора половина диагонали ОС=√(МC²-МО²)=√(100-64)=6 см
Тогда по т. о 3-х перпендикулярах ОН⊥ВС. ⇒ ∆ ОНС - прямоугольный, ОН=ОС•sin45°=6•√2/2=3√2 ⇒
МН=√(МО²+ОН²)=√(64+18)=√82 см
Диаметр АВ разделит хорду CD пополам: СМ = MD.
Обозначим СМ = MD = х.
MВ = AB - AM = 2·7 - 5 = 9 см.
По свойству хорд:
AM·MB = CM·MD
5·9 = x²
x = 3√5
СМ = MD = 3√5 см
CD = СМ + MD = 6√5 см
Объяснение: