Площадь боковой поверхности равна площади одной грани, умноженной на 3.
Площадь грани равна половине произведения апофемы на сторону основания или
S=(а²√3):4
1. Боковая грань - равносторонний треугольник, так как плоский угол при вершине равнобедренного треугольника равен 60 градусов
2. Апофему - гипотенуза - найдем из прямоугольного треугольника, образованного высотой пирамиды и одной третьей высоты основания - это катеты
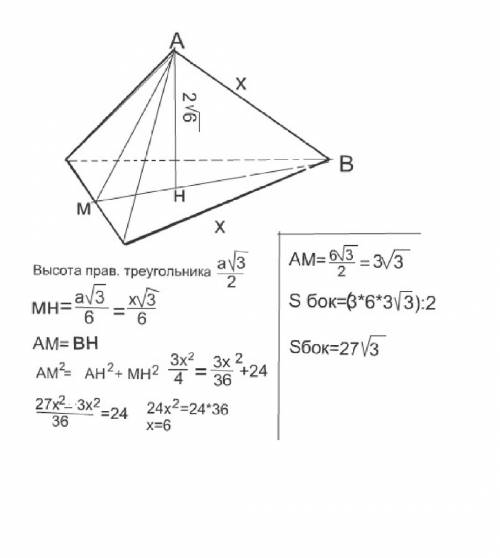
Для рассчетов примем сторону основания за х. Дальнейшее ренение дано
в рисунке, данном во вложении.
1) Построим линейный угол данного двугранного угла, для этого строим сечение плоскостью (А1В1СД) и доказываем, что угол А1ДА -линейный угол двугранного угла АДСА1. Докажем, что А1Д перпенд.ДС :СД перпенд.плоск.(АДД1), тогда СД перп. к любой прямой, лежащей в этой плоскости, а А1Д лежит в этой плоскости;
АД перпенд.ДС , т.к. АВСД - прямоугольник, таким образом лучи А1Д и АД перп. к ребру ДС, т.е. угол А1ДА - линейный
2)Из тр-ка АСД- прям.: АД=12 ( теор.Пифагора).
3) Из тр-ка АА1Д- прям.: тангенс А1ДА=12V3/12=V3
угол А1ДА = 60 град.