Question

Найдите угол между векторами a {3;1;−2} и b {−2;2; 0}

Answer 1

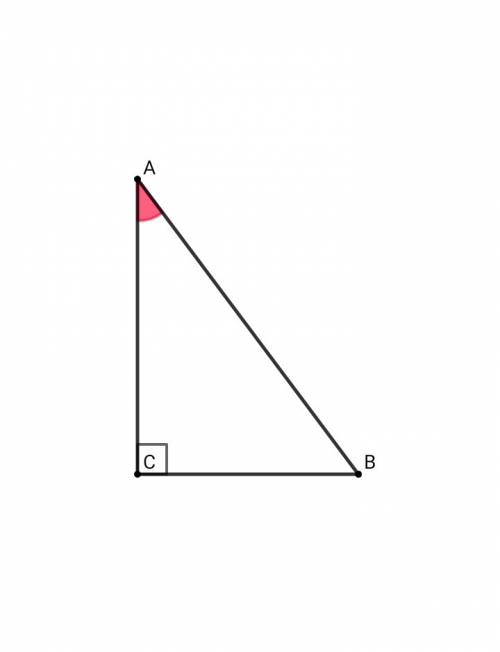
1) Найдем скалярное произведение векторов:

a·b= a_{x} *b_{x} + a_{y} * b_{y} =2·(-1) +3 · \frac{1}{2} =-2+ \frac{3}{2} = -\frac{1}{2}

2) Найдем длины векторов:

IaI= \sqrt{ a ^{2} _{x} +a ^{2} _{y}} = \sqrt{4+9} = \sqrt{13}

IbI= \sqrt{ b ^{2} _{x} +b ^{2} _{y}}= \sqrt{1+ \frac{1}{4} } = \sqrt{ \frac{5}{4} } = \frac{ \sqrt{5} }{2}

3) Найдем угол между векторами:

сos α = \frac{a*b}{|a|*|b|} = \frac{ -\frac{1}{2} }{ \sqrt{13}* \frac{ \sqrt{5} }{2} } = -\frac{ \sqrt{65} }{65}