Так как ни у одной из девочек имя не совпадает с названием их цветов, то Роза вырастила не розы, Маргарита - не маргаритки, а Анюта - не анютины глазки.
"Девочка, вырастившая маргаритки, обратила внимание Розы". - Из этого можно сделать вывод, что Роза вырастила не маргаритки. Значит, она вырастила анютины глазки.
Если Роза уже вырастила анютины глазки, это значит, что Маргарита не вырастила анютины глазки, а розы. Так, можно понять, что Анюта вырастила маргаритки.
ответ: Роза - анютины глазки, Маргарита - розы, Анюта - маргаритки.
ответ: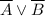 
.
Пошаговое объяснение:
Во-первых, как можно заметить, от C значение функции не зависит.
Особенно это хорошо видно на последних двух строчках. Если убрать переменную C, то получиться таблица из 4 строк:
A B F
0 0 1
0 1 1
1 0 1
1 1 0
Это таблица истинности для отрицания И: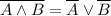 
- ответ.
На этом можно было бы остановиться (проверить по таблице истинности с учётом бесполезного С), но сделаем ещё кое-что - выведем это шаг за шагом, докажем, что С - бесполезная и никому не нужная переменная.
Запишем то же выражение в совершенной конъюнктивной нормальной форме. Выберем стоки, которые обращают выражение в Ложь.
A B C F
1 1 0 0
1 1 1 0
Две строки - две скобки. Единица в таблице означает отрицание переменной в скобке. Получаем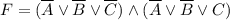 
.
Тут уже видно, что переменная С на результат не влияет. Упростим и приведём это к выражению выше.
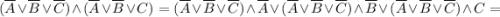
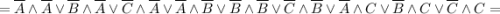
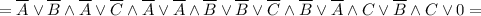
![= \overline A \lor \overline B \lor [(\overline B \land \overline A) \lor (\overline A \land \overline B)] \lor [(\overline C \land \overline A) \lor(\overline A \land C)] \lor [(\overline C \land \overline B) \lor (\overline B \land C)] =](/tpl/images/1360/3469/09f19.png)
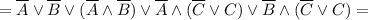
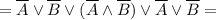
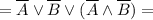
![= [(\overline A \lor \overline A) \land (\overline A \lor \overline B)] \lor \overline B =](/tpl/images/1360/3469/ce0d8.png)
![= [\overline A \land (\overline A \lor \overline B)] \lor \overline B =](/tpl/images/1360/3469/cc585.png)
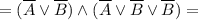
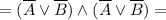
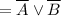- ответ.
Понятно, что тут нужен цикл для суммирования четырех членов вида
A²ˣ⁺¹ / [(2*х+1)*B²ˣ], х = 1, 2, 3, 4 и тут есть два варианта. Первый - считать, как написано. И на сегодня это правильный вариант, поскольку видна исходная формула. Второй - завести две добавочные переменные, в одну поместить A³, во вторую В². А затем получать следующие степени, домножая каждый раз на А² и В соответственно. Но это растянет программу и скроет исходную формулу от восприятия, что затруднит поиск ошибок. К счастью, современная версия языка Pascal - PascalABC.NET - обзавелась операцией возведения в степень и на ней прграмма будет выглядеть очень просто.
===== PascalABC.NET =====
begin
var (a, b) := ReadReal2('Введите А и В:');
var y := SeqGen(4, x -> A ** (2 * x + 1) /
((2 * x + 1) * B ** (2 * x)), 1).Sum;
y.Println
end.