Объяснение:
h,w = int(input().split())
c,p = int(input().split())
s = []
roadm = []
parks = []
cp = []
for i in range(1, h+1):
for j in range(1, w+1):
s.append([i,j])
for k in s:
if k[0]==1 or k[1]==1:
roadm.append(s.pop(k))
for t in s:
if t[0] == 2 or t[1] == 2:
cp.append(s.pop(t))
for y in s:
if y[0] == (f[0]+1 for f in cp) and y[1] == (f[1]+1 for f in cp) and y[0] == (f[0]-1 for f in cp) and y[1] == (f[1]-1 for f in cp):
parks.append(s.pop(y))
a = []
b = []
for o in s:
a.append(o[0])
b.append(o[1])
print(min(a))
print(min(b))
3:
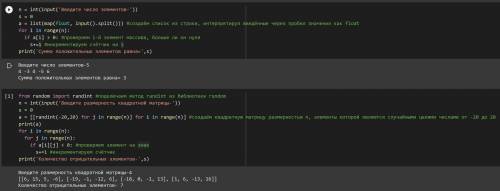
n = int(input('Введите число элементов-'))
s = 0
a = list(map(float, input().split())) #создаём список из строки, интерпретируя введённые через пробел значения как float
for i in range(n):
if a[i] > 0: #проверяем i-й элемент массива, больше ли он нуля
s+=1 #инкрементируем счётчик на 1
print('Сумма положительных элементов равна=',s)
4:
from random import randint #подключаем метод randint из библиотеки random
n = int(input('Введите размерность квадратной матрицы-'))
s = 0
a = [[randint(-20,20) for j in range(n)] for i in range(n)] #создаём квадратную матрицу размерностью n, элементы которой являются случайными целими числами от -20 до 20
print(a)
for i in range(n):
for j in range(n):
if a[i][j] < 0: #проверяем элемент на знак
s+=1 #инкрементируем счётчик
print('Количество отрицательных элементов-',s)
1) Переводим целую часть числа в двоичную СС:
29:2=14(1)
14:2=7(0)
7:2=3(1)
3:2=1(1)
Записываем цифры в скобках в одно число снизу вверх:
11101
Переводим дробную часть:
Умножаем дробную часть на основание системы счисления:
0,62*2=1,24(1)
В скобки записываем целую часть результата произведения, а дробную снова умножаем на основание системы счисления:
0,24*2=0,48(0)
Повторям эти действия, пока не достигнем нужной точности:
0,48*2=0,96(0)
0,96*2=1,92(1)
0,92*2=1,84(1)
0,84*2=1,68(1)
0,68*2=1,36(1)
0,36*2=0,72(0)
Записываем цифры в скобках сверху вниз:
0,10011110
В итоге:
11101,10011110 - это данное число в двоичной СС
2) аналогично первому
29:8=3(5)
35 - целая часть полученного числа
0,62*8=4,96(4)
0,96*8=7,68(7)
0,68*8=5,44(5)
0,475 - дробная часть полученного числа
В итоге:
35,475 - это данное число в восьмеричной СС