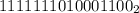Адресная сортировка
#include <iostream>
int main()
{
int value = 8;
int *ptr = &value;
std::cout << ptr << '\n';
std::cout << ptr+1 << '\n';
std::cout << ptr+2 << '\n';
std::cout << ptr+3 << '\n';
return 0;
}
Сортировка вставками
#include <iostream>
using namespace std;
int main()
{
const int N = 10;
int a[N] = { 12, 5, 3, 2, 45, 96, 6, 8, 11, 24 };
int buff = 0; // для хранения перемещаемого значения
int i, j; // для циклов
/ Начало сортировки /
for (i = 1; i < N; i++)
{
buff = a[i]; // запомним обрабатываемый элемент
// и начнем перемещение элементов слева от него
// пока запомненный не окажется меньше чем перемещаемый
for (j = i - 1; j >= 0 && a[j] > buff; j--)
a[j + 1] = a[j];
a[j + 1] = buff; // и поставим запомненный на его новое место
}
/ Конец сортировки /
for (int i = 0; i < N; i++) // вывод отсортированного массива
cout << a[i] << '\t';
cout << endl;
}
Думаю :)
представления целого числа со знаком называется "дополнительный код".
Алгоритм представления положительного числа:
1. Перевести число в двоичную систему счисления
2. Записать число в прямом коде в 16-ти двоичных разрядах
1.
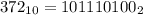
2.
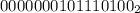(дополняем незначащими нулями до 15-ти разрядов и в старшем разряде ставим 0 в качестве знака положительного числа)
Представление числа: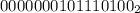
Алгоритм представления отрицательного числа:
1. Перевести модуль числа в двоичную систему счисления
2. Записать число в прямом коде в 16-ти двоичных разрядах
3. Найти обратный код (то есть инвертировать прямой код)
4. Найти дополнительный код, прибавив единицу к обратному коду
1.
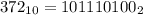
2.
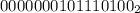(обычно дополняют незначащими нулями до 15-ти разрядов и в старшем разряде ставят 1 в качестве знака "-", но также допускается не выставлять значение 1 в знаковом разряде, а на следующем шаге проинвертировать все его разряды, не обращая внимания, знаковый ли это разряд или информационный. Я выбрал второй вариант)
3.
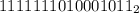(заменяем в прямом коде нули на единицы и наоборот)
4.
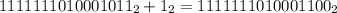
Представление числа: