1. Вычисляется сумма квадратов чисел от 1 до 4: 1²+2²+3²+4².
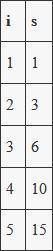
2. Вычисляется сумма чисел от 1 до 5. Таблица изменений S и i в цикле for прикреплена в первом вложении.
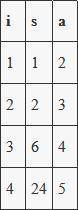
3. Здесь вычисляется произведение чисел от 1 до 4. После выполнения цикла for в s будет храниться 1*2*3*4=24, а в a - 5. Таблица изменений i, s и a в цикле for прикреплена во втором вложении.
4. Здесь вычисляется произведение чисел от 1 до 5, за исключением того, что изначально s=0, поэтому после цикла for в s тоже будет храниться 0. А в a будет храниться 6.
5. Это циклический алгоритм.
6. S=4. Внутри цикла while число S увеличивается на 1, пока не перестанет выполняться условие "X <= 3". Так как X увеличивается вместе с S, то после цикла S=X=4.
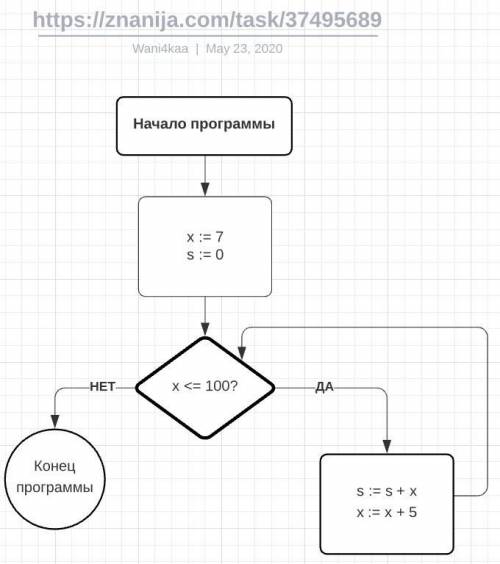
7. Не уверен, что соблюдены какие-то правила составления блок-схем, но в общем у меня получилась такая (вложение 3).
= - 127, максимальное число = + 127
2) Число 1607, ячейка двухбайтовая, один бит под знак, следовательно, под число отводится 15 бит, в двоичном представлении 1607(10) = 11001000111(2), дополняем до 16 бит, старший бит - знаковый - нулевой, так как число положительное
= 0000011001000111(2) - это двоичное представление в двухбайтовой ячейке, чтобы получить шестнадцатиричное представление, разбиваем число справа - налево по 4 бита
0000 0110 0100 0111 и записываем в шестнадцатиричном виде
0111(2) = 7(16) 0100(2) = 4(16) 0110(2) =6(16) 0000(2) = 0(16)
1607(16) = 0647(16) или без старшего не значащего нуля = 647(16)
3) для получения дополнительного кода числа, находят обратное число, или инверсию числа,
для этого каждый бит числа изменяют на противоположный, 1 на 0, 0 на 1
105(10) = 1101001(2) - это и есть дополнительный код числа - 105, т.е. дополнительным кодом
числа (- а) будет число а.
Найдем дополнительный код в однобайтовой ячейке числа 105(10) = 01101001(2),
а) находим обратное 01101001(2) ->(обратное) ->10010110(2)
б) дополнительный код-> обратный код + 1 ->(дополнительный)->10010111(2), а это число - 105
потому, что отрицательные числа представляются в дополнительном коде.
Если для числа - 105 найти дополнительный код, то получим число 105
10010111(2)->(дополнительный)->01101000+1->01101001 = 69(16) = 16*6+9 = 96+9 = 105