(см. объяснение)
Объяснение:
Число 21 в развернутой форме записи можно представить так:
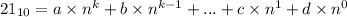
Из условия задачи следует, что последнее число в системе счисления с основанием n равно 0, т.е. 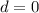 .
.
Тогда получим:
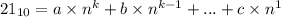
Заметим, что n можно вынести за скобки:
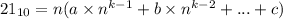
Разделим обе части равенства на n:
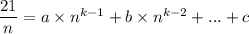
Получили, что 21 делится на основание системы счисления без остатка.
Учитывая, что n>1, наименьший делитель числа 21 - это 3.
Поэтому минимальное основание системы счисления, при записи числа 21 в которой последним символом будет 0 равно 3.
И действительно 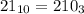 .
.
Задача решена!
Вот функция, определяющая, симметрична ли заданная квадратная матрица n-го порядка:
bool sym(int **mat, int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(mat[i][j] != mat[j][i]) {
return 0;
}
}
}
return 1;
}
Можете использовать её в своей программе:
#include <iostream>
int main() {
int n;
std::cin >> n;
int **a = new int *[n];
for(int i = 0; i < n; i++) {
a[i] = new int[n];
}
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
std::cin >> a[i][j];
}
}
std::cout << sym(a, n);
return 0;
}