Question

Сколько нулей содержится в троичной записи числа, которое можно представить в виде 81^1000-3^1600+3^800+2 ​

Answer 1

1598

Объяснение:

Рассмотрим данное выражение:

$81^{1000}-3^{1600}+3^{800}+2=3^{4000}-3^{1600}+3^{800}+3^{0}+3^{0}$

Подобное выражение - развернутая форма записи числа.

Здесь, например,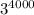 $3^{4000}$ степени выглядит в троичной системе счисления как 1 и четыре тысячи нулей после единицы, т.е. что-то вроде 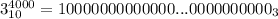$3^{4000}_{10}=10000000000000...0000000000_3$. Аналогично 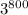$3^{800}$ в троичной системе счисления - это 1 и 800 нулей и так далее. Понятно, что, если единицы стоят в разных разрядах, выполнить сложение в любой системе счисления не составит труда, ведь 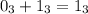$0_3+1_3=1_3$. Собственно, говоря, очевидно и, что 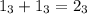$1_3+1_3=2_3$, но не забываем, что 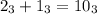$2_3+1_3=10_3$. Т.е. сначала выполним сложение. Еще раз замечу, что сложение выполняется в троичной системе счисления. Так, пока из 4000 нулей пропало 2, т.е. на данный момент осталось 3998 нулей. Но это еще не все. У нас есть вычитание. Вычитаем, понятно, по такому же принципу, как в десятичной системе счисления. Например, для десятичной системы счисления верно, что 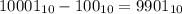$10001_{10}-100_{10}=9901_{10}$. Видим, что старшая единица пропадает, а нули меняются на 9, т.е. на основание системы счисления минус 1 (у нас 10-1=9). То же и в троичной системе. Например, 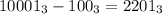$10001_3-100_3=2201_3$. Соответственно, в итоге в троичной системе счисления число примет вид: 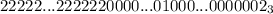$22222...2222220000...01000...0000002_3$, где сначала идет 2400 двоек (4000-1600), затем идет 799 нулей, затем единица, затем 799 нулей и в конце 2. ответим теперь на вопрос задачи: в троичной записи данного числа содержится 1598 нулей.

Задача решена!