6отрицательное целое число –710 записать в дополнительном коде в 16-разрядном представлении с указанием знака.

👇

Увидеть ответ

Ответ:

KaRaIcHiTaN

14.05.2023

сначало переводим это же число только со знаком плюс в двоичную систему счисления

7 = 0000000000000111 и дописываем впереди 13 нулей, т.к. нам нужен код в 16-разрядном представлении

теперь дописываем спереди бит отвечающий за знак

1,0000000000000111 пр.

теперь записываем обратный код, для этого нужно заменить все 0 на 1, а 1 на 0 за исключение бита отвечающего за знак

1,1111111111111000 обр.

теперь чтобы получить допонительный код нужно к обратному прибавить 1

1,1111111111111001 доп.

4,4(31 оценок)

Ответ:

VovanBah

14.05.2023

Преобразование числа из прямого кода в дополнительный осуществляется так:

Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

1) Записываем наше число в прямом(обычном двоичном коде в 16-разрядном представлении)

-7 в десятичной = 0000000000000111 - нули у нас впереди так как сетка 16 -разрядная

2) Инвертируем все разряды числа: 1111111111111000

3) Прибавляем к этому числу 1: 1111111111111001

4) Старший знаковый разряд у нас уже равен 1 следовательно число -7 в 10-ой в дополнительном коде: 1111110100111010

4,8(4 оценок)

Открыть все ответы

Ответ:

artem443090

14.05.2023

Объяснение:

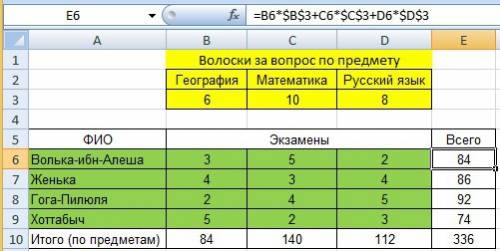
Условие i mod 2 = 0 означает, что i должно быть четным.

Условие i div 5 = 4 означает, что i находится в промежутке от 20 до 24 включительно.

Требуется сказать, какое последнее i было добавлено в сумму s, что сумма стала равной 424, а i удовлетворяет хотя бы одному из условий выше.

Найдем сумму четных чисел с 2 до 18 включительно.

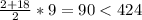$\frac{2+18}{2}*9=90$ - этого мало

Добавим еще сумму чисел от 20 до 24 включительно.

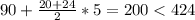$90+\frac{20+24}{2}*5=200$ - этого тоже мало.

Поэтому искомое значение i будет среди четных чисел больших 24.

Пусть количество четных элементов, начиная с 26, равно n, добавив которые к 200 можно получить 424. Тогда:

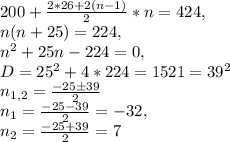
$200+\frac{2*26+2(n-1)}{2}*n=424,\\n(n+25)=224,\\n^2+25n-224=0,\\D=25^2+4*224=1521=39^2\\n_{1,2}=\frac{-25\pm39}{2}\\n_1=\frac{-25-39}{2}=-32,\\n_2=\frac{-25+39}{2}=7$

Среди найденных значений подходит только n=7.

Тогда последний требуемый четный элемент равен 26+2*(7-1)=38.

Таким образом, путем суммирования (2+4+...16+18)+(20+21+22+23+24)+(26+28+...+36+38) можно получить 424.

4,4(77 оценок)

Ответ:

ayazhanbeibit51

14.05.2023

Вариант 11 Дядя Федор, кот Матроскин и пес Шарик летом жили в Простоквашино, а папа с мамой слали им письма, посылки, телеграммы и бандероли, которые доставлял почтальон Печкин. Каждое письмо весило в среднем 100 г, каждая посылка - 5 кг, каждая телеграмма - 50 г, каждая бандероль - 500 г. Дядя Федор получил 10 писем, 2 посылки, 10 телеграмм и 1 бандероль. Кот Матроскин получил 4 письма, 1 посылку, 2 телеграммы и 1 бандероль. Пес Шарик не получил ни одного письма, ни одной телеграммы, зато получил 4 посылки и 2 бандероли.Построить электронную таблицу, из которой будет видно: сколько и какой почты получил каждый из трех жителей Про-стоквашино; сколько килограммов почты получил каждый из трех простоквашинпев; сколько весила вся доставленная Печкиным почта одного вида; какой общий груз пришлось перенести почтальону Печкину. смотри хls
Решить одну из , и сделать таблицу по информатике вариант 11 дядя федор, кот матроскин и пес шарик л