х=7690 - условие
var x, L, M: integer;
begin readln(x);
L:=0;
M:=0;
while x > 0 do begin
1) L:= L + 1 = 1;
M:= M + x mod 10 = 0;
x:= x div 10 = 7 69;
2) L:= L + 1 = 2;
M:= M + x mod 10 = 9;
x:= x div 10 = 7 6;
3) L:= L + 1 = 3;
M:= M + x mod 10 = 15;
x:= x div 10 = 7 ;
4) L:= L + 1 = 4;
M:= M + x mod 10 = 22;
x:= x div 10 = 0;
end;
writeln(L);
write(M);
end.
L = 4; M = 22
Объяснение:
1)L:= L + 1 = 0 + 1 = 1;
M:= M + x mod 10 = 0 + 0 (остаток) = 0;
x:= x div 10 = 7690 : 10 = 769 (остаток 0 здесь не пишется);
2)L:= L + 1 = 1 + 1 = 2;
M:= M + x mod 10 = 0 + 9 (остаток) = 9;
x:= x div 10 = 769 : 10 = 76 (остаток 9 здесь не пишется);
3)L:= L + 1 = 2 + 1 = 3;
M:= M + x mod 10 = 9 + 6 (остаток) = 15;
x:= x div 10 = 76 : 10 = 7 (остаток 6 здесь не пишется);
4)L:= L + 1 = 3 + 1 = 4;
M:= M + x mod 10 = 15 + 7 (остаток) = 22;
x:= x div 10 = 7 : 10 = 0 (остаток 7 здесь не пишется);
Не лишу себя удовольствия показать еще одно очень красивое и очень странное решение через словари.
n = int(input())
print({1<=n<=4: "Начальная школа",
5<=n<=9: "Среднее звено",
10<=n<=11: "Старшее звено"}[True])
Здесь мы создаем неименованный словарь, который в качестве ключа использует условное выражение, а в качестве значения - соответствующую этому выражению строку.
Когда мы тут же передаем ему в качестве ключа True, словарь начнет проверять ключи и вернет именно то значение, у которого выражение-ключ было истинным.
Сетевая тополо́гия — это конфигурация графа, вершинам которого соответствуют конечные узлы сети и коммуникационное оборудование, а рёбрам — физические или информационные связи между вершинами. Сетевая топология может быть физической — описывает реальное расположение и связи между узлами сети.
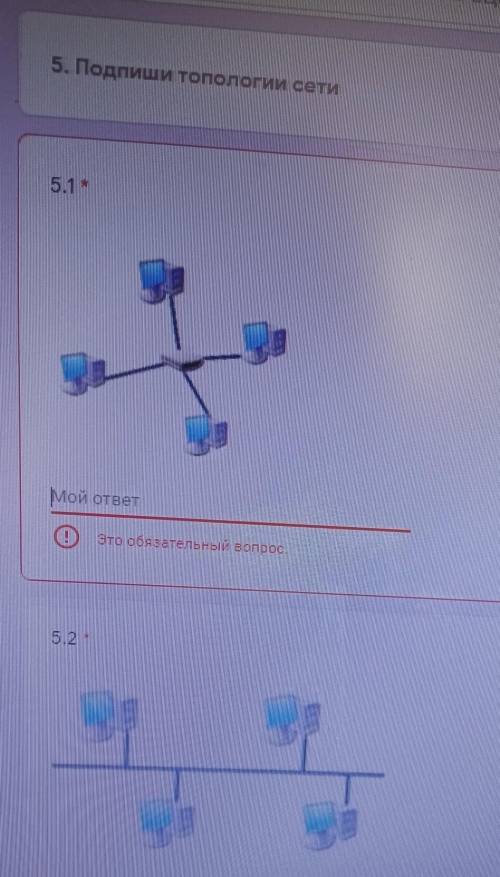
5.1 звездная топология
5.2 шинная топологи