1110001100(в двоичной системе)
Объяснение:
256+652=908
908:2=454(ост.0)
454:2=227(ост.0)
227:2=113(ост.1)
113:2=56(ост.1)
56:2=28(ост.0)
28:2=14(ост.0)
14:2=7(ост.0)
7:2=3(ост.1)
3:2=1(ост.1)
1110001100(в двоичной системе) =908(в десятичной)
Чтобы из десятичной системы число перевести в двоичную систему, то нам нужно будет делить число на 2,и так каждый раз, до тех пор, пока в ответе не будет 1
Далее собираем вот этот вот последний ответ 1,и все остатки(кстати, собираем мы это все снизу вверх), и получаем наше двоичное число
Удачи!
1. Двоичная система счисления похожа на привычную нам десятичную, за исключением того, что вместо десяти в ней используется основание 2 и всего две цифры, "1" и "0". Подробнее на этом сайте, там есть объяснение и все необходимое -> https://ru.wikihow.com/%D1%81%D0%BA%D0%BB%D0%B0%D0%B4%D1%8B%D0%B2%D0%B0%D1%82%D1%8C-%D0%B4%D0%B2%D0%BE%D0%B8%D1%87%D0%BD%D1%8B%D0%B5-%D1%87%D0%B8%D1%81%D0%BB%D0%B0 .
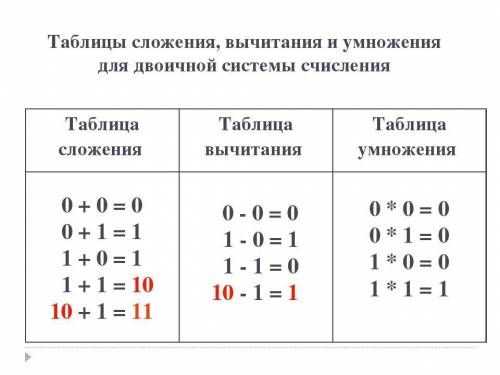
2. Сложение двоичных чисел. Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями.
Можно не использовать таблицу сложения в том случае, если хорошо запомнилась (там достаточно легко запоминать, гляди ниже на пикчу).
3. Подробнее на данном сайте -> https://ru.wikihow.com/%D0%B2%D1%8B%D1%87%D0%B8%D1%82%D0%B0%D1%82%D1%8C-%D0%B4%D0%B2%D0%BE%D0%B8%D1%87%D0%BD%D1%8B%D0%B5-%D1%87%D0%B8%D1%81%D0%BB%D0%B0 .
4. Сложения двойной системы счисления чисел такое же, как и в любой позиционной системе осуществления счисления суммы.
5. Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.
6. Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки). Подробно на данном сайте -> https://programforyou.ru/calculators/number-systems .
7. Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы.
309
Объяснение:
F(1) = 1
F(2) = 3
F(n) = F(n – 1) * n + F(n – 2) * (n – 1) при n > 2
Немного посчитаем подставляя значения n и предыдущих F(n)
n = 3 F(1) = 1 F(2) = 3
F(3) = F(3 – 1) * 3 + F(3 – 2) * (3 – 1) = F(2) * 3 + F(1) * 2 = 3 * 3 + 1 * 2 = 9 + 2 = 11
n = 4 F(2) = 3 F(3) = 11
F(4) = F(4 – 1) * 4 + F(4 – 2) * (4 – 1) = F(3) * 4 + F(2) * 3 = 11 * 4 + 3 * 3 = 44 + 9 = 53
n = 5 F(3) = 11 F(4) = 53
F(5) = F(5 – 1) * 5 + F(5 – 2) * (5 – 1) = F(4) * 5 + F(3) * 4 = 53 * 5 + 11 * 4 = 265 + 44 = 309