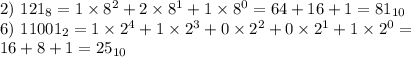
 , каждую восьмеричную цифру заменяем тремя двоичными (триадой) и получаем двоичное число. А затем, зная что
, каждую восьмеричную цифру заменяем тремя двоичными (триадой) и получаем двоичное число. А затем, зная что 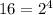 , мы группируем двоичные разряды справа налево по четыре, получая тетрады. И, наконец, каждую тетраду мы заменяем соответствующей шестнадцатиричной цифрой. Описывать этот процесс долго, а перевод делается быстро.
, мы группируем двоичные разряды справа налево по четыре, получая тетрады. И, наконец, каждую тетраду мы заменяем соответствующей шестнадцатиричной цифрой. Описывать этот процесс долго, а перевод делается быстро.
42
Объяснение:
F(1): вывод 1. Т.к. 1<5, произойдут рекурсивные вызовы
F(1+3)=F(4): вывод 4. Т.к. 4<5, произойдут рекурсивные вызовы
F(4+3)=F(7): вывод 7. Т.к. 7>5, рекурсивные вызовы не произойдут.
F(4*3)=F(12): вывод 12. Т.к. 12>5, рекурсивные вызовы не произойдут.
F(1*3)=F(3): вывод 3. Т.к. 3<5, произойдут рекурсивные вызовы
F(3+3)=F(6): вывод 6. Т.к. 6>5, рекурсивные вызовы не произойдут.
F(3*3)=F(9): вывод 9. Т.к. 9>5, рекурсивные вызовы не произойдут.
Сумма выведенных чисел будет равна 1+4+7+12+3+6+9=42