Описание алгоритма:
Будем наращивать длину последовательности от 0 знаков до N. Пусть после какого-то количества шагов у нас выписаны все последовательности длины А и мы хотим узнать количество подходящих последовательностей длины А+1. Распределим все последовательности на три группы(так как предыдущие символы нас не волнуют, то любые последовательности одной группы для нас равнозначны):
1) Заканчиваются на 0.
2) Ровно на одну единицу
3) Ровно на две единицы.
Из каждой последовательности группы 1 приписыванием нуля или единицы мы можем получить одну последовательность группы 1 и одну - группы 2. Неважно, какие именно, но они не перекрываются, т.к. предыдущие символы различны, хоть мы их и не учитываем. Точно так же из второй группы мы получаем одну последовательность группы 3 и одну группы 1, а из группы 3 - только группу 1. Таким образом, если количества последовательностей длины А по группам были (x, y, z), то для длины А+1 такое распределение будет (x+y+z, x, y). Если взять для длины 0 тройку (0, 0, 1) и просчитать тройки от 1 до N, получится искомое количество. Для N=1 и N=2 также работает правильно.
Программа на Pascal:
var num00,num01,num11,mem00:integer;
n,i:byte;
begin
readln(n);
num00:=1;
for i:=1 to n do begin
mem00:=num11;
num11:=num01;
num01:=num00;
num00:=num01+num11+mem00;
end;
writeln(num11+num01+num00);
end.
Рассмотрим два решения
Объяснение:
Т.к. нельзя пользоваться встроенными функциями, то обозначим собственные функции.
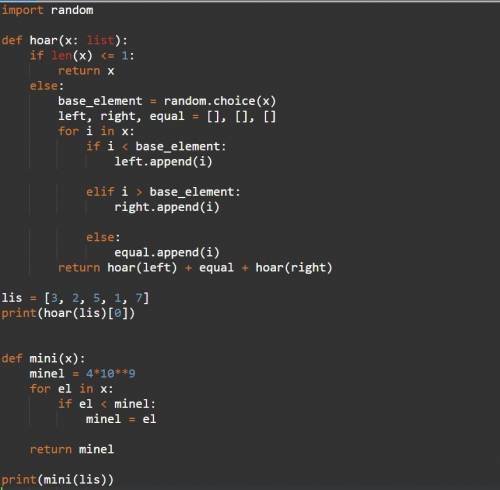
Функция mini() ищет минимальный элемент посредством сравнения всех элементов списка.
Однако у Вас (может быть, и не у вас) я видел вопрос на сортировку списка с своей функции. Предлагаю рассмотреть алгоритм Хоара, который используется во встроенной функции сортировки.
Алгоритм приведен на скриншоте.
Более того, чтобы найти минимальный элемент списка (отсортированного), достаточно просто взять первый его элемент (с индексом ноль)
a = int(input())
b = int(input())
s = a * b
p = a * 2 + b * 2
print(s)
print(p)
Объяснение:
Если компилятор выдаст ошибки, дай знать
Пишу с телефона, так что мог опечататься