46
Объяснение:
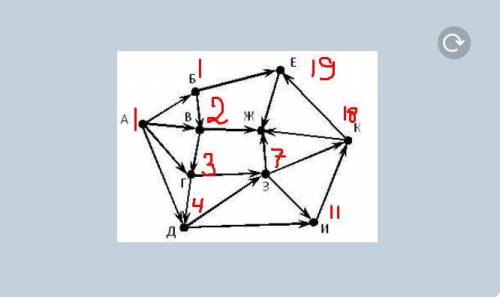
Будем последовательно находить количество дорог до пунктов, которые встречаются по пути к пункту Ж. Мы уже находимся в городе А, поэтому туда можно сказать ведет 1 дорога. ставим метку. От города А дороги идут в Б Г В и Д, но мы не можем сказать, сколько дорог ведет в города Г В и Д, потому что в них ведет по 2 дороги, из А и из Б/B/Г соответственно, а знаем мы только количество дорог в А(1). Поэтому ставим метку городу, которому мы ее можем дать - это город Б, в который ведет только 1 дорога из А. Количество дорог в какой-либо город равна сумме дорог в города, которые предшествуют ему. То есть в Б ведет тоже только 1 дорога. Помечаем.
По аналогии делаем со всеми другими городами:
Город В: в него ведут 2 дороги, из А и Б, суммируем количество дорог в них и получаем количество дорог в В, то есть 1+1=2.
Город Г: 2 дороги, из А и В, то есть количество дорог в г равно сумме дорог в А и В, то есть 1+2=3
И так далее. Рисунок со всеми метками прикреплен
Задача 2. после 6 применений 64 четных цифры (после каждого применения их количество увеличивается в 2 раза)
Задача 1. не может быть Даша второй, т.к. это утверждение в 4 и 5 строках. Не может быть третьей Ира (предполагается в 3 и 5 строках). Значит первая Маша. А Даша и Ира - не призеры. Из 4-й строки получаем. что и Боря не призер. Из 1 и 3 строки получаем, что Вася - не призер (т.к. указано что Вася второй и Вася третий). Значит призер Таня (не первая и не третья, значит - вторая). Из 2 строки получаем, что и Гена не призер. Остается Антон - третий
ответ: Маша, Таня, Антон
Задача 3. Всего можно составить 60 трехзначных чисел. Числе. меньших 200, 12. Вероятность 12/60=0,2
Задача 9. 16
Задача 4. Можно (Земля-Марс-юпитер-Венера-Меркурий)
Задача 6.
370
343
640
613
910
901
271
253
550