ответ: 123-45-67+89 = 100.
Объяснения:
Пусть минимальным рядом считается тот, в котором меньше слагаемых.
Для нахождения всех подходящих рядов, а так же минимального, напишем простую программу на Python.
Код:
#===============================
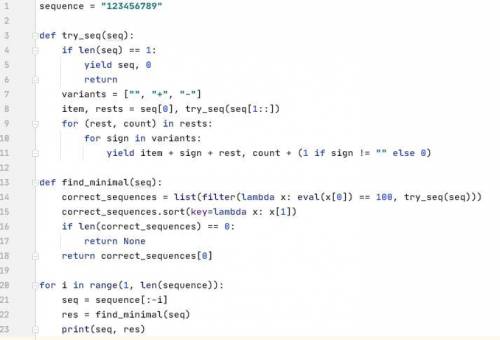
sequence = "123456789"
def try_seq(seq):
if len(seq) == 1:
yield seq, 0
return
variants = ["", "+", "-"]
item, rests = seq[0], try_seq(seq[1::])
for (rest, count) in rests:
for sign in variants:
yield item + sign + rest, count + (1 if sign != "" else 0)
def find_minimal(seq):
correct_sequences = list(filter(lambda x: eval(x[0]) == 100, try_seq(seq)))
correct_sequences.sort(key=lambda x: x[1])
if len(correct_sequences) == 0:
return None
return correct_sequences[0]
for i in range(1, len(sequence)):
seq = sequence[:-i]
res = find_minimal(seq)
print(seq, res)
#===============================
В данном коде обозначен генератор try_seq(), который получает на вход строку из первых 9 натуральных чисел.
В этом генераторе мы рекурсивно разбиваем строку на цифры и перебираем все возможные расстановки знаков (+, -, *нет знака*). Генератор позволяет получить все возможные комбинации без затрат на хранение самих последовательностей. На выходе из генератора получаем все возможные разбиения, которые теперь необходимо обработать.
Для обработки и выдачи минимального ряда используем функцию find_minimal(). В первую очередь нас интересуют те из них, которые в результате вычисления дают 100.
Пропускаем полученные значения через filter, сравнивая значения с 100. Оставшиеся значения сортируем по возрастанию количества разбивающих знаков в них.
Осталось только проверить подстроки от 123456789 до 1 на возможность существования ряда, дающего 100.
Для этого в цикле прогоняем подстроки через find_minimal().
Получаем, что ряд существует для 1234567, 12345678 и 123456789:
12345678 ('12+34-5+67-8', 4)
1234567 ('1+23+4+5+67', 4)
123456 None
12345 None
1234 None
123 None
12 None
1 None
Минимальная в данном случае: 1+23+4+5+67 для последовательности 1234567.
====================
Если ответ удовлетворил, не забудь отметить его как "Лучший".

Из города А можно попасть в города B-2, C-4, D-8, F-16.
16 - многовато. Поищем другие пути.
Если учесть, что мне не возвращаемся в посещенные точки, то всего можно насчитать 7 путей:
A-F = 16A-C-D-E-F = 17A-B-D-F = 8A-D-E-F = 18A-D-F = 11A-B-D-E-F = 15A-C-D-F = 10Оставляем только пути, которые проходят через точку E:
A-C-D-E-F = 17A-D-E-F = 18A-B-D-E-F = 15Рассчитывая стоимость путей, получаем, что минимальная длина пути = 15. (путь A-B-D-E-F).
ответ: 15
Если ответ устроил, то не забудь отметить его как "Лучший".