2), 3)
Объяснение:
8) Выражение состоит из двух частей, соединенных логическим И. Результат будет истинным, если обе части истинны.
Каждая из частей - дизъюнкция (логическое ИЛИ), она истинна, если хотя бы один из операндов истинен.
Если внимательно присмотреться, можно заметить, что если в одной части стоит какое-то xN, то в другой стороне - НЕ xN. Тогда в какую-то скобку каждое xN добавляет 1, в другую 0.
Не подходят только варианты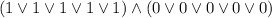 
или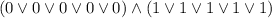 
, в остальных случаях в каждой из скобок будет хотя бы одна единица. Первый случай реализуется для (x1, x2, x3, x4, x5) = (0, 0, 0, 1, 1); второй - для (x1, x2, x3, x4, x5) = (1, 1, 1, 0, 0).
Всего есть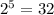 
комбинации из 5 двоичных переменных, 2 из них не подходят - остаётся 30.
10) Варианты 2 и 4 не подходят: во второй строчке x1 = 1, но 1 ИЛИ (...) = 1, а не 0.
1 тоже не подходит: это выражение имеет вид (...) И x3 И (...), но если x3 = 0 (последняя строчка), то всё выражение должно было бы быть 0.
15
Объяснение:
Изобразим схему дорог на рисунке.
Путь A-B-C-E имеет длину 15, попробуем убедиться, что путей короче не бывает (если вы думаете, что это очевидно, то вы почти наверняка забыли рассмотреть пути вида A-B-E-C-A-D-E, путей с многократными заходами в пункты тут много).
- Пусть C-E (длина 10) есть в маршруте. Тогда для более короткого маршрута длина остальных отрезков пути должна быть не больше 4, но наименьшие длины других отрезков 2 и 3, либо A-D длины 4. Не подходит, C-E отбрасываем - по нему путь короче 15 не проходит.
- Аналогично с A-C (длина 9): на оставшийся путь остается не больше 5. Но из C в E не попасть на 5, так как все отрезки, идущие в E, имеют длину не меньше 5, а тот, который имеет длину 5, начинается в B.
После отбрасывания остаются только 2 пути A-B-C-D-E и A-D-C-B-E, но эти пути длиннее 15.