Для определенности назову сами символы как-нибудь:
A (0.084), B (0.168), C (0.336), D (0.0336), E (0.3784)
Алгоритм Хаффмана:
- упорядочиваем символы по возрастанию
- сливаем вместе два символа с наименьшими вероятностями, получаем составной символ с вероятностью, равной сумме вероятностей
- повторяем, пока не останется один символ
По сути это строит дерево Хаффмана, но мне рисовать весь процесс не хочется, буду писать в строчку:
D (0.0336), A (0.084), B (0.168), C (0.336), E (0.3784) - сливаем D и A, получается (D, A) с вероятностью 0.0336 + 0.084 = 0.1176
(D, A) (0.1176), B (0.168), C (0.336), E (0.3784) - сливаем (D, A) и B, получается ((D, A), B) с вероятностью 0.1176 + 0.168 = 0.2856
((D, A), B) (0.2856), C (0.336), E (0.3784) - сливаем ((D, A), B) и C, получается (((D, A), B), C) с вероятностью 0.2856 + 0.336 = 0.6216
E (0.3784), (((D, A), B), C) (0.6216) - сливаем в (E, (((D, A), B), C)), для проверки: вероятность 0.3784 + 0.6216 = 1
(E, (((D, A), B), C)) (1)
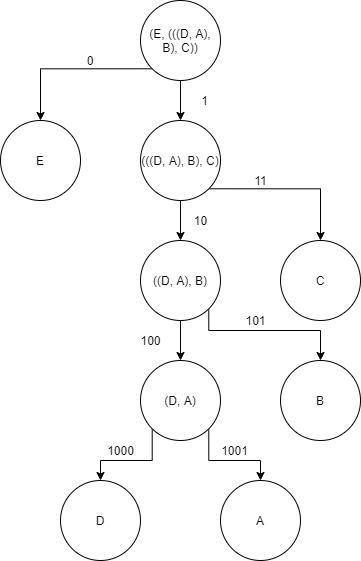
Готово! Если хочется перерисовать в виде бинарного дерева, у родителя (x, y) потомки x и у, мой вариант (для компактности он изображен немного искаженно) во вложении.
Осталось получить коды символов. Корню присваиваем пустой код, для левого потомка приписываем к коду родителя 0, для правого 1.
Получаем коды: A = 1001, B = 101, C = 11, D = 1000, E = 0.
Эффективность кодирования - это ожидаемая длина кода. Она в данном случае равна
0,084 * 4 + 0,168 * 3 + 0,336 * 2 + 0,0336 * 4 + 0,3784 * 1 = 2,0248 бит
Для сравнения, по формуле Шеннона количество информации в битах на один символ
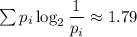
1)110010112+101112= x2 2)111012*11102= x2 №6 (110002+6A716)*518=x10 1) MMMCCCXXIX=300010+30010+2010+910= =332910 2) 235410=200010+30010+5010+410= =MMCCCVIV 1) 1101010012=42510 Проверка: 2) 79810= 11000111102 Проверка: 78910=14258 201110=7DB16 1)110010112+101112=111000102 2)111012*11102=1100101102 (110002+6A716)*518=(2410+170310)*4110=7080710 Вариант 2 Вариант 3 №1 1)MMMCDLXIX → x10 2)187810 р.с.с. → №2 1) MMDCCLXXV → x10 2) 135710 р.с.с. → №1 №2 (+проверка) (+проверка) 1)11011112 → x2 2)103810 → x10 1) 110110112 → x2 2)619 10 → x10 43210 → x8 №3 (+проверка) №4 (+проверка) 145610 → x16 №5 1)11001112+1101112= x2 2)11101112*11112= x2 №6 (110012+6216)*1018= x10 Вариант 4 59810 → x8 №3 (+проверка) №4 (+проверка) 126810 → x16 №5 1)1110010112+101012= x2 2)11001012*11012= x2 №6 (101112+25A16)*168= x10 Вариант 5 1)MMMDCCXLIX 2)1874 10 р.с.с. → №1 → x10 №2 1) MMCXCVII 2) 154310 р.с.с. → → x10 №1 №2 (+проверка) (+проверка) 1)110110110 2 2) 53210 → x2 → x10 67810 → x8 №3 (+проверка) №4 (+проверка) 134410 → x16 №5 1)11011102+110012= x2 2)110012*111012= x2 №6 1)11110001 2 → x2 2)650 10 → x10 №3 (+проверка) №4 (+проверка) 110110 → x8 56810 → x16 1)111000112+11102= x2 2)1110112*11112= x2 №5 №6 (1010112+AE216)*738= x10 (101112+FC16)*1528= x10 Вариант 6 1)MCMLXXXIII №1 → x10 Вариант 7 1)MMCDLXIX → x10 №1 2)187610 р.с.с. → 2) 190310 р.с.с. → №2 (+проверка) 1)1110111 2 → x2 2)712 10 → x10 №3 101010 → x8 (+проверка) №4 (+проверка) 100010 → x16 №5 1)111100112+11112= x2 2)11110112*10112= x2 №6 (101012+AC16)*10118= x10 Вариант 8 №1 → x10 1)MMCMXLVI 2) 177110 р.с.с. → №2 (+проверка) 1) 11101012 → x2 2) 33310 → x10 №3 66710 → x8 (+проверка) №4 (+проверка) 129810 → x16 №5 1)110011112+11112= x2 2)111012*110012= x2 (110012+EE16)*1248= x10 №6 Вариант 10 №1 1) MMMCDXLIV → x10 2)122210 р.с.с. → №2 (+проверка) 1)11000102 → x2 2) 33310 → x10 1)1101011 2 → x2 2) 60110 → x10 72810 → x8 190010 → x16 №2 (+проверка) №3 (+проверка) №4 (+проверка) №5 1)1111112+1010102= x2 2)1011112*1112= x2 №6 (111112+AE16)*2008= x10 Вариант 9 1) MMCCCLXXVIII 2) 220010 р.с.с. → №1 → x10 №2 (+проверка) 1) 111000112 → x2 2) 23110 → x10 №3 55510 → x8 150110 → x16 (+проверка) №4 (+проверка) №5 1)11000112+101112= x2 2)110012*1112= x2 №6 (111112+FA16)*10018= x10 Вариант 11 №1 1) MMDCCLXXXV → x10 2) 192810 р.с.с. → №2 (+проверка) 1) 111100102 → x2 2) 20210 → x10 99010 → x8 №3 (+проверка) №4 (+проверка) 150210 → x16 №5 1)11001112+11102= x2 2)101012*101012= x2 №6 (11012+CD16)*1118= x10 Вариант 12 №1 1) MMMCDXLV x→ 10 2) 311110→р.с.с. №2 (+проверка) 1)1100111 2 → x2 2) 18910 → x10 №3 50210 → x8 (+проверка) №4 (+проверка) 102510 → x16 №5 1)110011012+1112= x2 2)10111012*1012= x2 60610 → x8 190010 → x16 №3 (+проверка) №4 (+проверка) №5 1)110011112+1002= x2 2)1101112*11112= x2 (10102+AD16)*1108=x10 №6 Вариант 13 №1 1)MMCDXLIX 2)3053 10 р.с.с. → → x10 №2 (+проверка) 1)1100001 2 → x2 2) 19810 → x10 77710 → x8 №3 (+проверка) №4 (+проверка) 215610 → x16 1)11100012+1012= x2