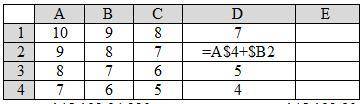
Вся сложность рекурсивных алгоритмов заключается в том, что внутри одной функции запустится другая.
Запускается F(5)
n>0? 5>0? - Да.
Выводится звёздочка, Запускается F(3), потом F(4), потом F(4) и снова выводится звёздочка (если все эти команды под условие попадают, а то у вас табуляция не расставлена)
На данный момент мы имеем 2 звёздочки и ещё 3 функции, которые должны быть выполнены.
Начнём с F(3)
3>0? Да. Тогда:
Выводится звёздочка, Запускается F(1), потом F(2), потом F(2) и снова выводится звёздочка
Уже 4 звёздочки
Нам осталось 2 раза выполнить F(2) (результаты у них будут одинаковые)
2 раза F(4) и F(1)
Запустим F(1):
1>0? Да.
Выводится звёздочка, Запускается F(-1), потом F(0), потом F(0) и снова выводится звёздочка
Звёздочек 6.
F(-1): -1>0? Нет. Ничего не делаем
F(0): 0>0? Нет. Ничего не делаем
F(2):
2>0
Выводится звёздочка, Запускается F(0), потом F(1), потом F(1) и снова выводится звёздочка
Уже 8 звёздочек
И 2 раза выводим F(1), а каждое F(1) даёт нам по 2 звёздочки
Итог: 12 звёздочек.
F(2) надо выполнить 2 раза, то бишь ещё 6 звёздочек, итог 18
Осталось 2 раза выполнить F(4)
4>0
Выводится звёздочка, Запускается F(2), потом F(3), потом F(3) и снова выводится звёздочка
20 звёздочек + 6 от F(2) + 16 от F(3) + 16 от F(3) = 58 звёздочек
F(4) выполняем второй раз 58+40=98 звёздочек - ответ
В дополнение прикреплю визуальное решение, оно должно быть попроще:
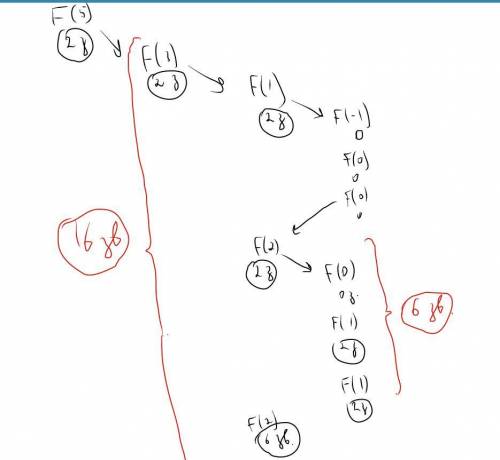
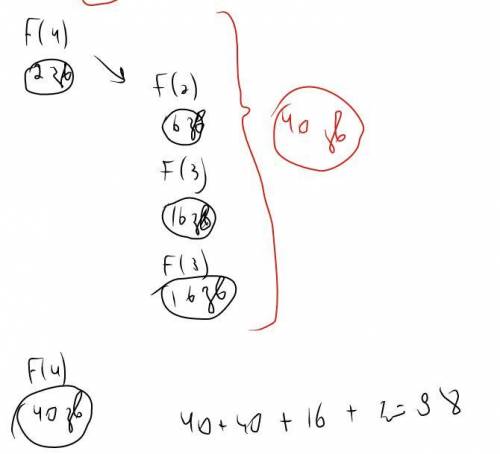
Объяснение:
Построить логическое выражение,
описывающее заштрихованную область
рассмотрим отрезки которые лежат на прямых
x=0;x=3;y=x;y=-x
по графику видно, что x≥0; x≤3; y≤x; y≥-x
(x≥0) and (x≤3) and (y≤x) and (y≥-x)
Построить область, описываемую
следующим логическим выражением
(x≥-2) and (x≤1) and (y≥-1) and (y≤2)
построим прямые x=-2;x=1;y=-1;y=2
x≥-2 область правее прямой x=-2 и точки на этой прямой
x≤1 область левее прямой x=1 и точки на этой прямой
y≥-1 область выше прямой y=-1 и точки на этой прямой
y≤2 область ниже прямой y=2 и точки на этой прямой
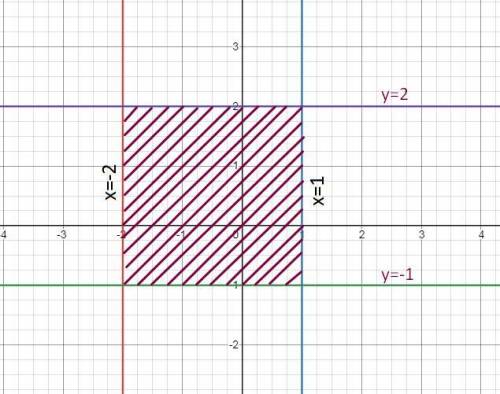
ответ: 13............