Объяснение:
const
max_elements = 1000;
a = 1;
b = 15;
first_file_name = '1.txt';
second_file_name = '2.txt';
var
i, j, n, r:integer;
p:real;
ar:array[1..max_elements] of integer;
f1, f2:text;
begin
randomize;
writeln('Input n = ');
readln(n);
for i:=1 to n do begin
ar[i]:=random(b-a+1)+a;
end;
assign(f1, first_file_name);
rewrite(f1);
for i:=1 to n do begin
writeln(f1, ar[i]);
end;
close(f1);
assign(f2, second_file_name);
rewrite(f2);
for i:=1 to n do begin
p:=1;
for j:=1 to i do
p:=p*ar[j];
writeln(f2, p:0:0);
end;
close(f2);
readln;
end.
3. B ∨ A
4. A & ¬(¬B ∨ C) ↔ A & B & ¬C (высказывания являются эквивалентными)
5. ложное
Объяснение:
3.
(¬A & B) ∨ (A & ¬B) ∨ (A & B) = (¬A & B) ∨ (A & B) ∨ (A & ¬B) = B & (¬A ∨ A) ∨ (A & ¬B) = B & 1 ∨ (A & ¬B) = B ∨ (A & ¬B) = (B ∨ A) & (B ∨ ¬B) = (B ∨ A) & 1 = B ∨ A
Согласно переместительному закону:
(¬A & B) ∨ (A & ¬B) ∨ (A & B) = (¬A & B) ∨ (A & B) ∨ (A & ¬B)
Согласно распределительному закону для логического сложения:
(¬A & B) ∨ (A & B) = B & (¬A ∨ A)
Согласно закону исключения третьего:
¬A ∨ A = 1
Согласно закону исключения констант для логического умножения:
B & 1 = B
Согласно распределительному закону для логического умножения:
B ∨ (A & ¬B) = (B ∨ A) & (B ∨ ¬B)
Согласно закону исключения третьего:
B ∨ ¬B = 1
Согласно закону исключения констант для логического умножения:
(B ∨ A) & 1 = B ∨ A
4.
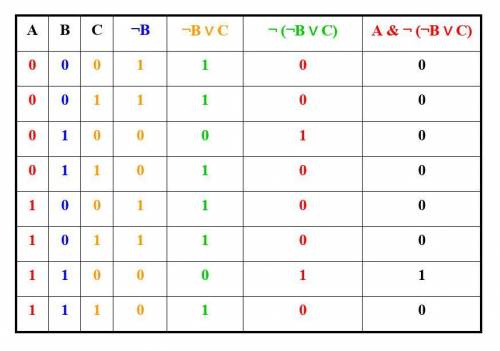
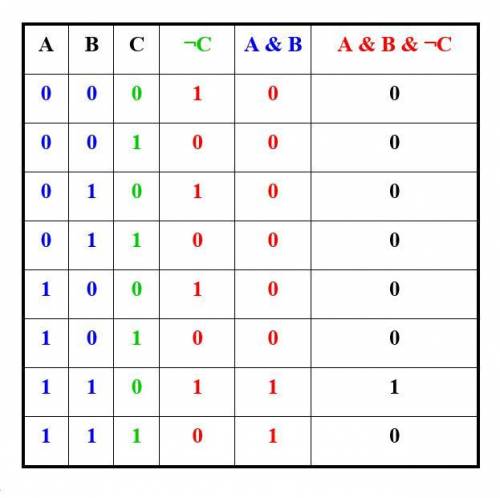
A & ¬(¬B ∨ C) = A & ¬(¬B) & ¬C = A & B & ¬C
Согласно закону де Моргана:
¬(¬B ∨ C) = ¬(¬B) & ¬C
Согласно закону двойного отрицания:
¬(¬B) = B
A & ¬(¬B ∨ C) ↔ A & B & ¬C
(высказывания являются эквивалентными)
Составим таблицы истинности для доказательства эквивалентности (картинки)
5.
(¬(X < 5) ∨ (X < 3)) & (¬(X < 2) ∨ (X < 1)) при X = 1
Подставим значение X в высказывание, а затем определим истинность или ложность
(¬(1 < 5) ∨ (1 < 3)) & (¬(1 < 2) ∨ (1 < 1)) = (¬(истина) ∨ (истина)) & (¬(истина) ∨ (ложь)) = (ложь ∨ истина) & (ложь ∨ ложь) = истина & ложь = ложь
Общий порядок действий:
1) скобки
2) НЕ (¬, черта над выражением) - значение противоположно исходному высказыванию
3) И (&, ∧) - истинно, когда оба исходных высказывания истинны
4) ИЛИ (∨) - ложно, когда оба исходных высказывания ложны
Основні етапи комп'ютерного моделювання: постановка задачі та її аналіз, побудова інформаційної моделі, розробка методу й алгоритму дослідження моделі, розробка комп'ютерної моделі, проведення комп'ютерного експерименту.