1) Цикл for(счётчик), выполняется от 1 до 5, через шаг 1. Результат выполнение: выполнится 4 раза т.к до 5 не дойдёт,
D = 120 поделится на 1, и так 4 раза.
2) Цикл while, выполняется пока A=1 меньше A(1) < 100, если условие верно, то цикл переходит на (1+2)*2=6, теперь A это 6. И так будет происходить, пока A меньше 100, если больше 100, то просто вывод.
3) Цикл while, S=0 N=1, потом S=S+N(0=0+1 = 1), потом N=N+3(1=1+3 = 4), дальше условие если N(4) меньше или не равно 15, то переходит к той же самой инструкции выше, пока N(4) меньше 15.
3)Программа на Python 3.7.2 Цикл while.
A = 1
while A < 100:
A = (A + 2) * 2
print(A)
ответ Объяснение:
Будем считать, что вершины четырехугольника пронумерованы, за каждой закреплен постоянный номер. Тогда задача сводится к подсчету числа разных расположения 4 букв на 4 местах (вершинах).
Для решения данной задачи воспользуемся формулой из комбинаторики, которая определяет число перестановок.
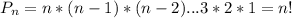
Из формулы следует, что количество которыми можно расположить 4 буквы на 4 вершинах:
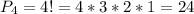
Число которыми 4 буквы можно разместить на 4 вершинах равно 24.
*4! - факториал 4. Факториалом числа 4 называют произведение всех натуральных чисел, меньше или равных 4.
Тогда условие будет иметь вид: (a+b=n) или (a=n) или (b=n), где а меняется от 1 до 9, b меняется от 0 до 9.
var
n, a, b: integer;
begin
Write('Введите число n -> '); Readln(n);
for a := 1 to 9 do
for b := 0 to 9 do
if (a + b = n) or (a = n) or (b = n) then Write(a, b, ' ');
Writeln
end.
Тестовое решение:
Введите число n -> 7
16 17 25 27 34 37 43 47 52 57 61 67 70 71 72 73 74 75 76 77 78 79 87 97