36.
Объяснение:
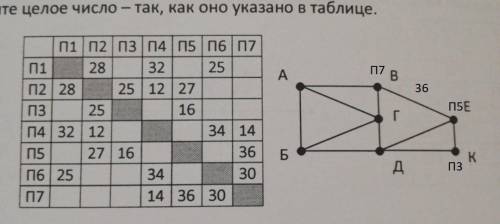
1. Ищем путь в таблице, который является уникальным, то есть отличается количеством путей. Таким пунктом является "П3", так как только у него есть два пути.
Ищем на схеме пункт с двумя путями. Это пункт "К". Отмечаем его, как "П3".
Итого получаем: "К" - "П3".
2. Смотрим какие пункты соединены с "П3". Это пункты "П2" и "П5".
У пункта "П2" 4 пути, у пункта "П5" 3 пути.
Ищем на схеме пункт, который связан с "К" и имеет 3 пути (берем именно три, так как нам нужно расстояние от В до Е, где В имеет три пути). Это пункт "Е". Отмечаем его, как "П5".
Итого получаем: "К" - "П3", "Е" - "П5".
3. Ищем в таблице пункт, который связан с "П5" и имеет три пути. "П2" не подходит, так как имеет 4 пути, "П3" мы уже соотнесли с "К". Подходит пункт "П7", так как он имеет три пути и связан с "П5". Соотнесем пункт "В" с "П7".
Итого получаем: "К" - "П3", "Е" - "П5", "В" - "П7".
Так как мы нашли пункты, которые соответствую В и Е, то можем найти расстояние между ними. В итоге, расстояние равно 36.
const
n=5;
var
a:array[1..n,1..n]of integer;
i,j:integer;
begin
for i:=1 to n do
begin
writeln;
for j:=1 to n do
begin
a[i,j]:=i+j;
write(a[i,j]:4);
end;
end;
end.
2)
const
n=4;m=5;
var
a:array[1..n,1..m]of integer;
i,j,max:integer;
begin
for i:=1 to n do
begin
writeln;
for j:=1 to m do
begin
a[i,j]:=random(100)-50;
write(a[i,j]:4);
end;
end;
max:=a[1,1];
for i:=1 to n do
for j:=1 to m do
if a[i,j]>max then
max:=a[i,j];
writeln;
writeln(max);
for i:=1 to n do
for j:=1 to m do
if (a[i,j]<0)and(a[i,j]>-5)then
a[i,j]:=max;
writeln;
for i:=1 to n do
begin
writeln;
for j:=1 to m do
write(a[i,j]:4);
end;
end.