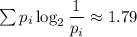Elektron raqamli imzo — Elektron hujjatdagi mazkur elektron hujjat axborotini elektron raqamli imzoning yopiq kalitidan foydalangan holda maxsus oʻzgartirish natijasida hosil qilingan hamda elektron raqamli imzoning ochiq kaliti yordamida elektron hujjatdagi axborotda xatolik yoʻqligini aniqlash va elektron raqamli imzo yopiq kalitining egasini identifikatsiya qilish imkoniyatini beradigan imzo. (qonun)Qonunda talab etilgan shartlarga rioya etilgan taqdirda elektron raqamli imzo qogʻoz hujjatga shaxsan qoʻyilgan imzo bilan bir xil ahamiyatga egadir. Elektron maʼlumotlarni kriptografik oʻzgartirish natijasida hosil qilingan belgilar ketma-ketligi. Elektron raqamli imzo maʼlumotlar blokiga qoʻshib qoʻyiladi va blokni qabul qiluvchiga, manbani va maʼlumotlarning butunligini tekshirish hamda soxtalashtirishdan muhofazalanish imkonini beradi. Hozirgi kunga kelib, ayrim mamlakatlar qonunchilik yoʻli bilan raqamli imzodan foydalanishni layoqatliligini qonunlashtirib qoʻyganlar. Elektron raqamli imzo kalitlari sertifikatlari roʻyxatga olish markazlari tomonidan beriladi.
Для определенности назову сами символы как-нибудь:
A (0.084), B (0.168), C (0.336), D (0.0336), E (0.3784)
Алгоритм Хаффмана:
- упорядочиваем символы по возрастанию
- сливаем вместе два символа с наименьшими вероятностями, получаем составной символ с вероятностью, равной сумме вероятностей
- повторяем, пока не останется один символ
По сути это строит дерево Хаффмана, но мне рисовать весь процесс не хочется, буду писать в строчку:
D (0.0336), A (0.084), B (0.168), C (0.336), E (0.3784) - сливаем D и A, получается (D, A) с вероятностью 0.0336 + 0.084 = 0.1176
(D, A) (0.1176), B (0.168), C (0.336), E (0.3784) - сливаем (D, A) и B, получается ((D, A), B) с вероятностью 0.1176 + 0.168 = 0.2856
((D, A), B) (0.2856), C (0.336), E (0.3784) - сливаем ((D, A), B) и C, получается (((D, A), B), C) с вероятностью 0.2856 + 0.336 = 0.6216
E (0.3784), (((D, A), B), C) (0.6216) - сливаем в (E, (((D, A), B), C)), для проверки: вероятность 0.3784 + 0.6216 = 1
(E, (((D, A), B), C)) (1)
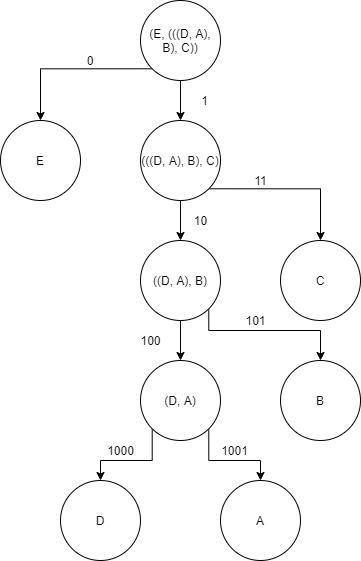
Готово! Если хочется перерисовать в виде бинарного дерева, у родителя (x, y) потомки x и у, мой вариант (для компактности он изображен немного искаженно) во вложении.
Осталось получить коды символов. Корню присваиваем пустой код, для левого потомка приписываем к коду родителя 0, для правого 1.
Получаем коды: A = 1001, B = 101, C = 11, D = 1000, E = 0.
Эффективность кодирования - это ожидаемая длина кода. Она в данном случае равна
0,084 * 4 + 0,168 * 3 + 0,336 * 2 + 0,0336 * 4 + 0,3784 * 1 = 2,0248 бит
Для сравнения, по формуле Шеннона количество информации в битах на один символ