8D
Объяснение:
1) Решение по простому. Шестнадцатиричная система это 4 бита на один знак. У нас двоичная запись 10001101. Всего 8 бит. Значит младшие 4 бита это младшее шестнадцатиричное число, а старшие 4 бита это старшее число. Смотрим на первые 4 бита 1101 это 1*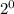 +0*
+0*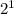 +1*
+1*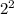 +1*
+1*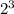 =1*1+0*2+1*4+1*8=1+4+8=13(в десятичной)=D (A-10, B-11, C-12, D-13 в 16-ричной).
=1*1+0*2+1*4+1*8=1+4+8=13(в десятичной)=D (A-10, B-11, C-12, D-13 в 16-ричной).
Смотрим на старшую четверку битов 1000=0*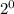 +0*
+0*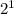 +0*
+0*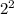 +1*
+1*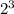 =0+0+0+8=8.
=0+0+0+8=8.
Пишем старшую цифре потом младшую 8D.
2)Теперь решение как нужно делать правильно (для любого основания). 10001101=1*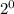 +0*
+0*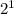 +1*
+1*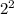 +1*
+1*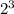 +0*
+0*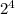 +0*
+0*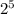 +0*
+0*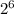 +1*
+1*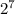 =1*1+0*2+1*4+1*8+0*16+0*32+0*64+1*128=1+4+8+128=141 (это перевели в десятичную). Затем переводим в нужную нам 16-ричную (это основание 16 значит будем делить на 16). 141/16= 8,8125. Мы получили целую часть от деления - цифра 8. Она у нас будет старшей (если при первом делении получилось число больше основания т.е.16 нужно его еще разделить). Умножим 8 на основание и вычтим это число из первоначального. 141-8*16=141-128=13. Мы получили младший разряд. Переводим 13 в 16-ричную (как показал ранее А-10 и т.д.). Получили ответ 8D
=1*1+0*2+1*4+1*8+0*16+0*32+0*64+1*128=1+4+8+128=141 (это перевели в десятичную). Затем переводим в нужную нам 16-ричную (это основание 16 значит будем делить на 16). 141/16= 8,8125. Мы получили целую часть от деления - цифра 8. Она у нас будет старшей (если при первом делении получилось число больше основания т.е.16 нужно его еще разделить). Умножим 8 на основание и вычтим это число из первоначального. 141-8*16=141-128=13. Мы получили младший разряд. Переводим 13 в 16-ричную (как показал ранее А-10 и т.д.). Получили ответ 8D
Объяснение:
В цифровой схемотехнике цифровой сигнал - это сигнал, который может принимать два значения, рассматриваемые как логическая "1" и логический "0".
Логические схемы могут содержать до 100 миллионов входов и такие гигантские схемы существуют. Представьте себе, что булева функция (уравнение) такой схемы была потеряна. Как восстановить её с наименьшими потерями времени и без ошибок? Наиболее продуктивный разбить схему на ярусы. При таком записывается выходная функция каждого элемента в предыдущем ярусе и подставляется на соответствующий вход на следующем ярусе. Этот анализа логических схем со всеми нюансами мы сегодня и рассмотрим.
// Внимание! Если программа не работает, обновите версию!
begin
var s:set of integer:=[];
for var i:=1 to 254 do begin
var flag:=True;
var j:=2;
var r:=round(sqrt(i));
while flag and (j<=r) do
if i mod j = 0 then flag:=false
else j+=1;
if flag then
if i mod 4=3 then s+=[i]
end;
foreach var x in s do Print(x);
end.
Результат
83 79 167 163 251 71 67 151 239 59 139 227 47 223 43 131 127 211 31 23 199 19 107 103 191 11 7 3 179