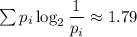
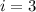
что нельзя:
1)В интернете нельзя лазять по разным не проверенным сайтам
2)Нельзя скачивать какие либо вещи с не проверенных сайтов
3)Нельзя делится местоположением своего дома и когда Вы куда либо уезжаете
4)Нельзя использовать простые пароли которые можно угадать
5)Нельзя использовать одни и те же пароли
6)Нельзя кликать по ссылкам на письмах от людей которых вы не знаете, и на непроверенных сайтов
7)Не используйте не безопасное соединение VPN
8)Не совершайте покупки на непроверенных сайтов
9)Не переписывайтесь с подозрительными незнакомцами
10)Не скачивайте ничего без антивируса
Объяснение:
что можно:
1)Можно сидеть на проверенных сайтах
2)Можно скачивать разные вещи с проверенных сайтов
3)Можно переписываться с людьми которые проверенные и точно никак не плохие
4) Можно использовать безопасное соединение VPN
5)Можно совершать покупки на проверенных сайтах
6)Ставить разные пароли на разные соцсети
7)Ставить не свою дату рождения, не свое имя не свое фото на аватарку
8)Можно переходить по ссылкам в письмах от знакомых вам людей
9)скачать антивирус
10) обмен чем либо с проверенными людьми
надеюсь ❤️
Для определенности назову сами символы как-нибудь:
A (0.084), B (0.168), C (0.336), D (0.0336), E (0.3784)
Алгоритм Хаффмана:
- упорядочиваем символы по возрастанию
- сливаем вместе два символа с наименьшими вероятностями, получаем составной символ с вероятностью, равной сумме вероятностей
- повторяем, пока не останется один символ
По сути это строит дерево Хаффмана, но мне рисовать весь процесс не хочется, буду писать в строчку:
D (0.0336), A (0.084), B (0.168), C (0.336), E (0.3784) - сливаем D и A, получается (D, A) с вероятностью 0.0336 + 0.084 = 0.1176
(D, A) (0.1176), B (0.168), C (0.336), E (0.3784) - сливаем (D, A) и B, получается ((D, A), B) с вероятностью 0.1176 + 0.168 = 0.2856
((D, A), B) (0.2856), C (0.336), E (0.3784) - сливаем ((D, A), B) и C, получается (((D, A), B), C) с вероятностью 0.2856 + 0.336 = 0.6216
E (0.3784), (((D, A), B), C) (0.6216) - сливаем в (E, (((D, A), B), C)), для проверки: вероятность 0.3784 + 0.6216 = 1
(E, (((D, A), B), C)) (1)
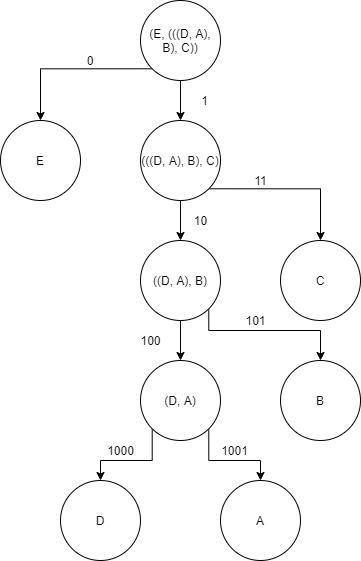
Готово! Если хочется перерисовать в виде бинарного дерева, у родителя (x, y) потомки x и у, мой вариант (для компактности он изображен немного искаженно) во вложении.
Осталось получить коды символов. Корню присваиваем пустой код, для левого потомка приписываем к коду родителя 0, для правого 1.
Получаем коды: A = 1001, B = 101, C = 11, D = 1000, E = 0.
Эффективность кодирования - это ожидаемая длина кода. Она в данном случае равна
0,084 * 4 + 0,168 * 3 + 0,336 * 2 + 0,0336 * 4 + 0,3784 * 1 = 2,0248 бит
Для сравнения, по формуле Шеннона количество информации в битах на один символ