1) 221₃ = 25₁₀
2) 444₅ = 124₁₀
3) 232₄ = 46₁₀
4) 1000₂ = 8₁₀
Объяснение:
1) 222₃ = 2 * 3² + 2 * 3¹ + 2 * 3⁰ = 2 * 9 + 2 * 3 + 2 * 1 = 18 + 6 + 2 = 26₁₀
222₃
-
1₃
221₃
221₃ = 2 * 3² + 2 * 3¹ + 1 * 3⁰ = 2 * 9 + 2 * 3 + 1 * 1 = 18 + 6 + 1 = 25₁₀
2) 1000₅ = 1 * 5³ + 0 * 5² + 0 * 5¹ + 0 * 5⁰ = 1 * 125 + 0 * 25 + 0 * 5 + 0 * 1 = 125₁₀
1000₅
-
1₅
444₅
1. Занимаем 1 из 1 остаётся 0 (в следующий разряд переносится 10₅)
2. Занимаем 1 из 10 остаётся 4₅ (в следующий разряд переносится 10₅, 10₅ - 1₅ = 4₅)
3. Занимаем 1 из 10 остаётся 4₅ (в следующий разряд переносится 10₅, 10₅ - 1₅ = 4₅)
4. Вычитаем 1 из 10 получаем 4₅ (10₅ - 1₅ = 4₅)
444₅ = 4 * 5² + 4 * 5¹ + 4 * 5⁰ = 4 * 25 + 4 * 5 + 4 * 1 = 100 + 25 + 4 = 124₁₀
3) 233₄ = 2 * 4² + 3 * 4¹ + 3 * 4⁰ = 2 * 16 + 3 * 4 + 3 * 1 = 32 + 12 + 3 = 47₁₀
233₄
-
1₄
232₄
232₄ = 2 * 4² + 3 * 4¹ + 2 * 4⁰ = 2 * 16 + 3 * 4 + 2 * 1 = 32 + 12 + 2 = 46₁₀
4) 1001₂ = 1 * 2³ + 0 * 2² + 0 * 2¹ + 1 * 2⁰ = 1 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 8 + 1 = 9₁₀
1001₂
-
1₂
1000₂
1000₂ = 1 * 2³ + 0 * 2² + 0 * 2¹ + 0 * 2⁰ = 1 * 8 + 0 * 4 + 0 * 2 + 0 * 1 = 8 + 1 = 8₁₀
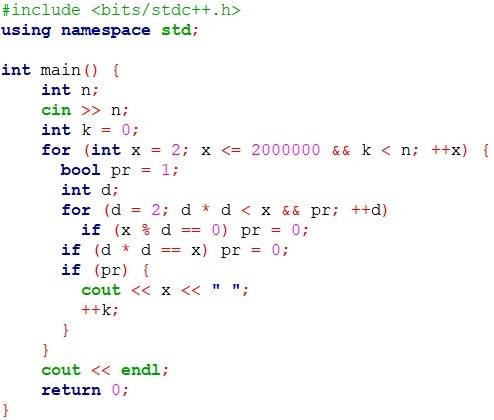
Пока мы не набрали n простых чисел, будем перебирать числа от 2 до ... и пытаться разложить их на множители.
Код вложен в ответ.
Решето Эратосфена позволяет быстро находить все простые числа на отрезке ![[2; x]](/tpl/images/0959/5527/0be77.png) (в нашем случае x - какая-то константа).
(в нашем случае x - какая-то константа).
Пусть x равен 25.
Тогда идея такова: запишем все числа от 2 до 25.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
По умолчанию все числа помечены как простые. Конкретно здесь числа, помеченные как составные, будут показываться в нижних индексах: ₂₅
Берем первое число 2. Оно помечено как простое. От квадрата этого числа до x помечаем все числа, делящиеся на 2, как составные:
2 3 ₄ 5 ₆ 7 ₈ 9 ₁₀ 11 ₁₂ 13 ₁₄ 15 ₁₆ 17 ₁₈ 19 ₂₀ 21 ₂₂ 23 ₂₄ 25
Берем следующее число, помеченное как простое. Это 3. От квадрата этого числа до x помечаем все числа, делящиеся на 3, как составные:
2 3 ₄ 5 ₆ 7 ₈ ₉ ₁₀ 11 ₁₂ 13 ₁₄ ₁₅ ₁₆ 17 ₁₈ 19 ₂₀ ₂₁ ₂₂ 23 ₂₄ 25
Следующее простое число - 5. От квадрата пяти до x помечаем все числа, кратные 5, как составные:
2 3 ₄ 5 ₆ 7 ₈ ₉ ₁₀ 11 ₁₂ 13 ₁₄ ₁₅ ₁₆ 17 ₁₈ 19 ₂₀ ₂₁ ₂₂ 23 ₂₄ ₂₅
Квадрат всех остальных простых чисел больше x. Решето построено.
КодПеревернем массив, представляющий решето. В composite[i] хранится true, если i - составное, false иначе.
#include <bits/stdc++.h>
using namespace std;
const int x = 2000000;
bool composite[x + 1];
void calc() {
for (long long i = 2; i <= x; ++i)
if (!composite[i] && (i * i <= x))
for (long long j = i * i; j <= x; j += i)
composite[j] = true;
}
int main() {
calc();
int n;
cin >> n;
int k = 0;
for (int i = 2; i <= x && k < n; ++i)
if (!composite[i]) {
cout << i << " ";
++k;
}
cout << endl;
return 0;
}
var n,i,k,j,f:longint;
a:array [1..10000] of longint;
begin
k:=0;
read (n);
a[1]:=1;
a[2]:=1;
for i:=3 to 10000 do
begin
if not(a[i-1] < n) then
begin
break
end;
a[i]:=a[i-1]+a[i-2];
k:=k+1
end;
for i:= 1 to k do
begin
f:=0;
for j:=2 to a[i]-1 do
if a[i] mod j=0 then f:=1;
if f=0 then write (a[i],' ');
end;
end.
Это для Pascal