1, 2, 3, 4
Объяснение:
Введем обозначения:
a = X > 0, b = X > 4
Тогда выражение будет иметь вид (a + b) → b и нужно найти условия, когда оно ложно. Вместо этого, мы будем искать, когда отрицание этого условия истинно, т.е. истинность ¬( (a + b) → b)
Для начала избавимся от импликации
¬( ¬(a + b) + b)
А теперь примерим к внешнему отрицанию закон де-Моргана
(a + b) · ¬b
Раскрываем скобки
a · ¬b + b · ¬b
a · ¬b + 0
a · ¬b
Делаем обратную замену
( X > 0) · ¬(X > 4)
( X > 0) · (X ≤ 4)
Переведем это на более понятный язык:
X > 0 И X ≤ 4, или
0 < X ≤ 4
Из целых чисел сюда подойдут 1, 2, 3, 4.
1, 4
Объяснение:
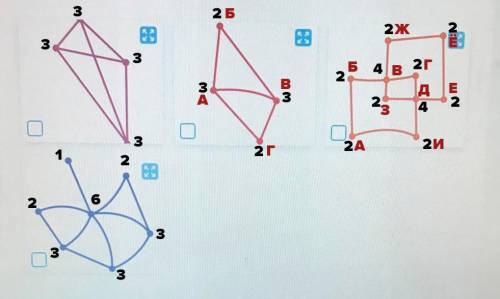
Рассмотрим путь по такому городу, который проходит по каждой улице не более чем по одному разу.
Простое наблюдение: если какая-то площадь не является началом или концом пути, то из неё должно вести чётное число дорог: по одной дороге в город нужно войти, из другой выйти, и так каждый раз.
Значит, в если в городе есть больше двух городов, из которых ведут нечетное число дорог, то его нельзя обойти, пройдя по каждой улице один раз, так что они точно понравились мистеру Фоксу.
На рисунке черным цветом указано число дорог для каждой площади. Получается, что города 1 и 4 мистеру Фоксу понравились. В городах 2 и 3 можно предложить маршрут, который проходит по каждой улице по одному разу: для 2 это, например, АБВАГВ, для 3 АБВГДЕЁЖВЗДИА - так что эти города понравились мистеру Фоксу не так сильно.
2 Красный голубой фиолетовый зелёный жёлтый жёлтый
3 Собакакот кролик морская свинка...
4(2;4;6;8;10;24;48)