Модели объектов и процессов можно разбить на пять групп: вербальные, математические, кибернетические, табличные, графические.
Под вербальными моделями понимаются описательные модели в цифровом виде, пригодном для обработки на компьютере. В эту группу входят и математические модели, доведенные до стадии алгоритма.
Кибернетические модели — это модели, использующие принцип «чёрного ящика». О внутреннем содержании этого состояния можно судить, подавая сигналы на вход «ящика» и наблюдая его реакцию на выходе из «ящика».
В группу табличных информационных моделей попадают электронные таблицы видов «объект - свойство», «объект - объект» и «двоичная матрица». В каждой строке таблицы «объект - свойство» содержится информация об одном объекте или одном событии. В таблицах «объект - объект» отображаются взаимосвязи между разными объектами. В таблицах «двоичная матрица» отображается качественный характер связи между объектами.
В группе графических информационных моделей выделяют четыре вида моделей: схемы, чертежи, карты, графы. Графы, в свою очередь, разбиты на две категории — иерархические системы и сети.
Решение проверка условий Фано):
1) Для однозначного декодирования достаточно, чтобы выполнялось условие Фано или обратное условие Фано;
2) Проверяем последовательно варианты 1, 3 и 4; если ни один из них не подойдет, придется выбрать вариант 2 («это невозможно»);
3) Проверяем вариант 1: А–00, Б–01, В–011, Г–101, Д–111.
«прямое» условие Фано не выполняется (код буквы Б совпадает с началом кода буквы В);
«обратное» условие Фано не выполняется (код буквы Б совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит;
4) Проверяем вариант 3: А–00, Б–010, В–01, Г–101, Д–111.
«прямое» условие Фано не выполняется (код буквы В совпадает с началом кода буквы Б);
«обратное» условие Фано не выполняется (код буквы В совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит;
5) Проверяем вариант 4: А–00, Б–010, В–011, Г–01, Д–111.
«прямое» условие Фано не выполняется (код буквы Г совпадает с началом кодов букв Б и В); но «обратное» условие Фано выполняется (код буквы Г не совпадает с окончанием кодов остальных буквы); поэтому этот вариант подходит;
ответ: 4
Решение дерево):
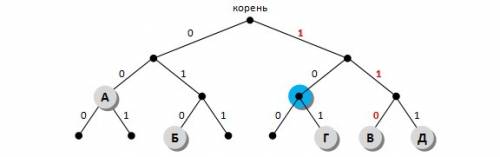
1) Построим двоичное дерево, в котором от каждого узла отходит две ветки, соответствующие выбору следующей цифры кода – 0 или 1; разместим на этом дереве буквы А, Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах, составляющих путь от корня до данной буквы (красным цветом выделен код буквы В – 011):
однозначность декодирования получается за счёт того, что при движении от корня к любой букве в середине пути не встречается других букв (выполняется условие Фано);
3) Теперь проверим варианты ответа: предлагается перенести одну из букв, Б, В или Г, в узел с кодом 01, выделенный синим цветом
4) Видим, что при переносе любой из этих букв нарушится условие Фано; например, при переносе буквы Б в синий узел она оказывается на пути от корня до В, и т.д.; это значит, что предлагаемые варианты не позволяют выполнить прямое условие Фано
5) Хочется уже выбрать вариант 2 («это невозможно»), но у нас есть еще обратное условие Фано, для которого тоже можно построить аналогичное дерево, в котором движение от корня к букве дает её код с конца (красным цветом выделен код буквы В – 011, записанный с конца):
видно, что обратное условие Фано также выполняется, потому что на пути от корня к любой букве нет других букв
6) В заданных вариантах ответа предлагается переместить букву Б, В или Г в синий узел; понятно, что Б или В туда перемещать нельзя – перемещённая буква отказывается на пути от корня к букве Г; а вот букву Г переместить можно, при этом обратное условие Фано сохранится
ответ: 4
program senya;
var
a1, a2, a3, a4: integer;
begin
for a1 := 1 to 9 do
for a2 := 0 to 9 do
for a3 := 0 to 9 do
for a4 := 0 to 9 do
if (a1 * 1000 + a2 * 100 + a3 * 10 + a4) mod 133 = 125 then
writeln (a1,a2,a3,a4);
if (a1 * 1000 + a2 * 100 + a3 * 10 + a4) mod 134 = 111 then
writeln (a1,a2,a3,a4);
end.