6) щелочи: NaOH, KOH, LiOH,Ca(OH)2
нерастворимые: Ti(OH)3, Mg(OH)2
9) KOH + HNO3= H2O + KNO3
n=m÷M
n(HNO3) = 18,9÷63= 0,3 моль
по уравнению следует, что: n(HNO3)= n(KNO3)=0,3 моль
m=n×M
m(KNO3) = 0,3 × 101= 30,3 г
ответ:30,3г
10) из дано этот элемент щелочноземельный металл, все ЩЗМ реагируют с азотом одинаково(азот восстанавливается до -3), примем щзм за Х:
3X+N2=X3N2
n= V÷Vm
(для газов при н.у. Vm=22,4 л/моль)
n(N2) = 1,12:22,4= 0,05 моль
по уравнению реакции: 3×n(N2)= n(X)
n(X)= 0,05×3= 0,15 моль
M=m÷n
M(X)=3,6÷0,15=24г/моль => Х - это Мg
схема электронного строения на фото
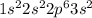
6) щелочи: NaOH, KOH, LiOH,Ca(OH)2
нерастворимые: Ti(OH)3, Mg(OH)2
9) KOH + HNO3= H2O + KNO3
n=m÷M
n(HNO3) = 18,9÷63= 0,3 моль
по уравнению следует, что: n(HNO3)= n(KNO3)=0,3 моль
m=n×M
m(KNO3) = 0,3 × 101= 30,3 г
ответ:30,3г
10) из дано этот элемент щелочноземельный металл, все ЩЗМ реагируют с азотом одинаково(азот восстанавливается до -3), примем щзм за Х:
3X+N2=X3N2
n= V÷Vm
(для газов при н.у. Vm=22,4 л/моль)
n(N2) = 1,12:22,4= 0,05 моль
по уравнению реакции: 3×n(N2)= n(X)
n(X)= 0,05×3= 0,15 моль
M=m÷n
M(X)=3,6÷0,15=24г/моль => Х - это Мg
схема электронного строения на фото
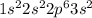
Закон сохранения массы означает, что в ходе реакции масса не изменяется. Значит умма масс продуктов реакции всегда равна сумме масс исходных реагентов.
Объяснение:
B покоящейся системе законы сохранения массы и энергии означают, что внутри системы они могут превращаться, оставаясь в совокупности неизменными. Если система состоит из нескольких компонентов k и одной фазы Ф, то при отсутствии химических взаимодействий по закону сохранения массы сумма масс всех компонентов должна быть равна массе всей системы:
М1 + М2 +….+ Мn = М или
Если система имеет несколько (m) фаз Ф И один компонент, то по закону сохранения массы сумма масс всех фаз должна быть равна общей массе системы:
МФ1 + МФ2 +….+ МФn = М или
Из последнего выражения закона сохранения массы следует, что чем больше станет масса одной фазы, тем меньше будет масса другой, но сумма масс всех фаз останется неизменной. С рассмотренных выше двух предельных случаев можно получить балансовые уравнения для каждого компонента и каждой фазы, участвующих в процессе.Обычно в процессах все вещества находятся в движении или, как принято говорить, в потоке. Под потоком понимают перемещение какой-либо среды в пространстве. Наиболее часто инженеру-технологу приходится иметь дело с конвективными потоками, которые характеризуются движением множества частиц под действием какой-либо силы из одного места пространства в другое. Если конвективный поток отнесен к единице площади, через которую он переносится, то говорят о плотности конвективного потока. Плотность потока является вектором, направление которого совпадает с направлением движения потока.
Размерность плотности потока [q] = [ед. количества/(м2с)].
Для характеристики любой системы достаточно трех потоков: массы (или компонента), теплоты (или энтальпии) и импульса.
В тех случаях, когда баланс составляют для части аппарата или малой области пространства (например, при выводе дифференциальных уравнений), существенными могут быть не только конвективные, но и молекулярные составляющие потоков - например, за счет диффузии (если среда, протекающая через рассматриваемый объем, имеет неравномерное распределение концентраций).
Законы сохранения массы, энергии и импульса обычно рассматривают совместно. Поэтому и подход к составлению балансов этих субстанций должен быть идентичным.