1. Запишем схему этой реакции:
Cu + HNO3 = Cu (NO3)2 + NO2↑ + H2O
2. Расставим степени окисления всех элементов в веществах, участвующих в реакции:
Cu0 + H+N+5O-23 = Cu+2(N+5O-23)2 + N+4O-22↑ + H+2O-2
Степени окисления поменяли медь и азот.
3. Составляем схему, отражающую процесс перехода электронов:
N+5+е- = N+4 окислитель, процесс восстановление
Cu0 -2е- = Cu+2 восстановитель, процесс окисление
4. Уравняем число отданных и принятых электронов. Для этого находим наименьшее общее кратное для чисел 1 и 2. Это 2. В результате деления наименьшего общего кратного на число отданных и принятых электронов, находим коэффициенты перед окислителем и восстановителем.
N+5+е- = N+4 2
Cu0 -2е- = Cu+2 1
5. Переносим коэффициенты в исходную схему и преобразуем уравнение реакции.
Cu + ?HNO3 = Cu (NO3)2 + 2NO2↑ + 2H2O
Азотная кислота участвует не только в окислительно-восстановительной реакции, поэтому коэффициент сначала не пишется. В результате, окончательно получается следующее уравнение:
Cu + 4HNO3 = Cu (NO3)2 + 2NO2↑+ 2H2O
Объяснение:
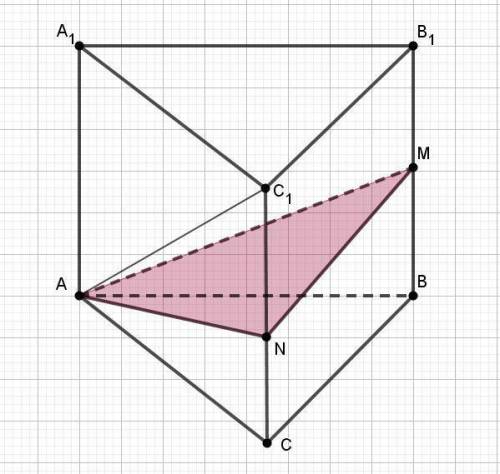
1) Сечение строится по заданным точкам.
Точку N находим в соответствии со свойством биссектрисы (см. пункт 2). Ребро СС1 точкой N делится в отношении 3:5.
2) По заданию AN является биссектрисой угла CAC1.
Диагональ АС1 боковой грани по Пифагору равна √(6² + 8²) = 10.
Примем СN = х.
По свойству биссектрисы х/6 = (8 - х)/10. Сократим знаменатели на 2.
24 - 3х = 5х,
8х = 24,
х = 24/8 = 3.
По заданию ВМ = 8/2 = 4.
Сечение AMN от призмы отсекает пирамиду с основанием BCNM, которое является трапецией (CN ║BM).
S(BCNM) =((3+4)/2)*6 = 21 кв.ед.
Высота H этой пирамиды равна высоте основания АВС.
H = 6*cos 30° = 6*√3/2 = 3√3.
V1 = V(ABCNM) = (1/3)*21*3√3 = 21√3 куб.ед.
Площадь основания призмы So = 6²√3/4 = 9√3 кв.ед.
Объём призмы V = 9√3*8 = 72√3 куб.ед.
Объём отсечённой части призмы равен V2 = 72√3 - 21√3 = 51√3 куб.ед.
ОтношениеV1/V2 = 21√3/51√3 = 7/17.
Объяснение: