Вобещем, вот так как то( на обращяй внимание на зачеркнутое).)))
1. Площадь квадрата равна длине его стороны, возведённой в квадрат: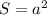 
, где 
- это сторона квадрата. Зная площадь, можем вычислить длину стороны: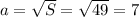 
см. Периметр квадрата равен длине его стороны, умноженной на 4: 
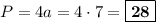см.
2. Периметр прямоугольника равен удвоенной сумме его смежных сторон. Пусть см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть,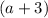 
см. Составляем уравнение:
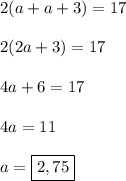
Тогда другая сторона его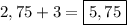 
см.
Площадь прямоугольника равна произведению длин его смежных сторон, тогда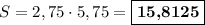 
см².
3. Для начала найдём вторую сторону прямоугольника. Периметр прямоугольника равен удвоенной сумме его смежных сторон, тогда:
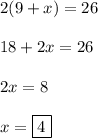
Тогда площадь прямоугольника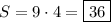 
см².
Прямоугольник имеет такую же площадь, что и квадрат. Площадь квадрата равна длине его стороны, возведённой в квадрат: 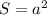, где - это сторона квадрата. Зная площадь, можем вычислить длину стороны: 
см. Периметр квадрата равен длине его стороны, умноженной на 4: 
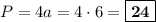см.
x > 2
Пошаговое объяснение:
Данное неравенство равносильно следующей системе:
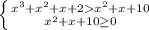
Первое неравенство системы - исходное, возведенное во вторую степень
Второе неравенство - ограничение на существование(т.к левая часть больше правой, которая неотрицательная, то условие на существование левой части можно не учитывать).
Запишем второе неравенство в виде уравнения и убедимся, что корней нет . Т.к. (D < 0), значит, парабола лежит выше оси Oy,следовательно, нет никаких ограничений на x.
В первом неравенстве системы получаем :
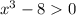- разность кубов, которая раскладывается следующим образом:
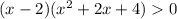
Второй множитель больше 0 при всех x из множества R, значит, достаточно, чтобы только x-2 > 0, то есть, x > 2
1) -0,5
2) -2,3
3) -3,1
1) -0,1
2) -11,6
3) -0,7
Пошаговое объяснение: