Гюльназ потратила на уборку квартиры 11/20 часа, что на 2/15 частей больше чем мытье посуды сколько всего времени потратила гюльназ на уборку и на мытье посуды6 класс умираю
1) Находим первую производную функции: y' = -3x²+12x+36 Приравниваем ее к нулю: -3x²+12x+36 = 0 x₁ = -2 x₂ = 6 Вычисляем значения функции на концах отрезка f(-2) = -33 f(6) = 223 f(-3) = -20 f(3) = 142 ответ: fmin = -33, fmax = 142 2) a) 1. Находим интервалы возрастания и убывания. Первая производная равна f'(x) = - 6x+12 Находим нули функции. Для этого приравниваем производную к нулю - 6x+12 = 0 Откуда: x₁ = 2 (-∞ ;2) f'(x) > 0 функция возрастает (2; +∞) f'(x) < 0функция убывает В окрестности точки x = 2 производная функции меняет знак с (+) на (-). Следовательно, точка x = 2 - точка максимума. б) 1. Находим интервалы возрастания и убывания. Первая производная. f'(x) = -12x2+12x или f'(x) = 12x(-x+1) Находим нули функции. Для этого приравниваем производную к нулю 12x(-x+1) = 0 Откуда: x1 = 0 x2 = 1 (-∞ ;0) f'(x) < 0 функция убывает (0; 1) f'(x) > 0 функция возрастает (1; +∞) f'(x) < 0 функция убывает В окрестности точки x = 0 производная функции меняет знак с (-) на (+). Следовательно, точка x = 0 - точка минимума. В окрестности точки x = 1 производная функции меняет знак с (+) на (-). Следовательно, точка x = 1 - точка максимума.
3. Исследуйте функцию с производной f(x)=2x^2-3x-1 1. D(y) = R 2. Чётность и не чётность: f(-x) = 2(-x)² - 3*(-x) - 1 = 2x² + 3x - 1 функция поменяла знак частично. Значит она ни чётная ни нечётная 3. Найдём наименьшее и наибольшее значение функции Находим первую производную функции: y' = 4x-3 Приравниваем ее к нулю: 4x-3 = 0 x₁ = 3/4 Вычисляем значения функции f(3/4) = -17/8 Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную: y'' = 4 Вычисляем: y''(3/4) = 4>0 - значит точка x = 3/4 точка минимума функции. 4. Найдём промежутки возрастания и убывания функции: 1. Находим интервалы возрастания и убывания. Первая производная равна f'(x) = 4x-3 Находим нули функции. Для этого приравниваем производную к нулю 4x-3 = 0 Откуда: x₁ = 3/4 (-∞ ;3/4) f'(x) < 0 функция убывает (3/4; +∞) f'(x) > 0 функция возрастает В окрестности точки x = 3/4 производная функции меняет знак с (-) на (+). Следовательно, точка x = 3/4 - точка минимума
1) 3/4 часа это 60мин/4 * 3= 15 * 3 =45мин 50мин-45мин=5 мин
2) х=3у у=х-24 подставляем х-24 в верхнее уравнение вместо у: х=3*(х-24) х=3х-72 переносим 3х через знак =, при этом у него появляется знак минус х-3х=-72 -2х=-72 минусы взаимно сокращаются, х=36, проверка подтверждает. 3) 18+12=30 это было всего конфет если уже учили решать пропорции, то так: 30конфет-это 100% 12 конфет- х %. перемножаем числа крест-накрест, получаем 30х=1200 х=40 % если пропорции не учили, то 12/30 *100= 40%
4) решая уравнение. нужно как можно меньше чисел оставлять там, где х. переносим 2 через знак=, то есть умножаем 2*4, получается: 20-4х=8 оставляем -4х, переносим 20 через знак =. при этом по правилам перед 20 появляется минус. -4х=8-20 -4х=-12 минусы взаимно сокращаются х=12/4 х=3
Приведём дроби к общему знаменателю:
Теперь мы можем узнать, сколько времени ушло на мытьё посуды:
ответ: на уборку ушло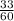
частей, на мытьё - 
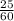частей.
Так же, если целое 60, то можно представить что это час, а значит:
ответ: на уборку ушло 33 минуты, а на мытьё - 25 минут.