Объем призмы ищется по такой формуле:
V = Sосн * h, где Sосн — площадь основания призмы, h — ее высота.
Так как все ребра призмы равны, то h = 6 см и в ее основании лежит равносторонний треугольник. Площадь равностороннего треугольника можно найти по следующей формуле:
S = a²√3 / 4, где a — сторона треугольника.
Воспользуемся ей и найдем площадь основания призмы, зная, что a = 6 см:
Sосн = 6²√3 / 4 = 9√3 см².
Теперь можно найти объем призмы:
V = 9√3 * 6 = 54√3 ≈ 93,5 см³.
ответ: объем прямой треугольной призмы равен примерно 93,5 см³.
Пошаговое объяснение:
1) По формуле сложения сворачиваем, получается:
cos (128+52)=cos 180= -1
2) Я, так понимаю, косинус найти нужно?
Если так, то:
применяем основную тригонометрическую формулу sin^2 x+cos^2 x =1, подставляем все известные и решаем:
cos^2 x=1-(144/169)
cos^2 x=25/169
cosx = 5/13, но поскольку косинус во 2 четверти отрицательный, то ответ -5/13
3)2sin+sqrt2 = 0 (sqrt - корень)
2sin = -sqrt2
sin = -sqrt2/2
x=(-1)^k+1 * 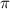 /4+2
/4+2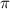 n, n
n, n  z
z
4) tg^2 x - tgx = 0
Выносим tgx за скобку:
tgx(tgx-1)=0
tgx=0 tgx-1=0
x = 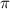 n, n
n, n  z tgx=1
z tgx=1
x=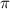 /4+
/4+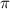 n, n
n, n  z
z
5 11/14 или 5.7