– каждому действительному простому корню b соответствует частное решение вида
eᵇˣ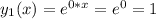
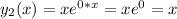
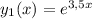
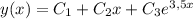
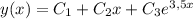
– каждому действительному простому корню b соответствует частное решение вида
eᵇˣ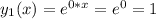
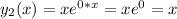
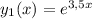
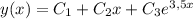
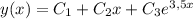
Решение. Пусть Н — основание высоты пирамиды (рисунок 2). Тогда точка
Н совпадает с центром основания ABCD, a поэтому НА=НВ=НС=HD=
1 AC 2 Тем самым точка Н совпадает с центром окружности,
описанной около основания ABCD. Рассмотрим плоскость AS С и
найдем на высоте SH точку О такую, что OS=ОА (рисунок 3). Так как
SH AC , AH 2 , и AS=3, то SH 32 (
2)2 7 . Обозначим
SO=R. Тогда OH 7 R и
AO2 AH 2 OH 2 2 (
7 R)2 9 2
7R R2 . Из условия АО=R
составляем уравнение: 9 2
7R R2 R2 . Отсюда R
Рассматривая треугольники АНО, ВНО, СНО, DHO, получаем, что они
прямоугольные и равны, так как имеют соответственно равные катеты.
Отсюда АО=ВО=СО=DO=SO. Поэтому сфера с центром О и радиусом
9
7 .содержит все вершины пирамиды.
14
ответ: R
9
7 .
14