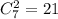выбрать одно элементарное событие из 6^7 возможных, так, чтобы пятерка выпала только в двух испытаниях. Вероятность каждого из таких событий - это произведение вероятностей двукратного выпадения 5 и пятикратного выпадения не 5, то есть 
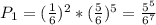. Умножая на число событий, получаем, что вероятность искомого события равна 
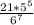, или приблизительно 23,44%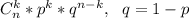
s=vt; s которое проехал автомобилист= 5x, а расстояние, которое проехал
V=s/t
20/1=20 км/ч скорость машины
1) пусть x- скорость автомобилиста, тогда скорость мотоциклиста x-20;
мотоциклист= 7(x-20) так как расстояние они проехали одинаковое мы их
велосипедист= 6(х-25), так как расстояние они проехали одинаковое мы их
20/(1/4)=5 км/ч скорость лыжника
s которое проехал мотоциклист= 2,25x, а расстояние, которое проехал
v=s/t
велосипедиста= 40-25=15.
приравниваем 2,25х=6(х-25) отсюда x=40( скорость мотоциклиста).Скорость
2)пусть x- скорость мотоциклиста, тогда скорость велосипедиста x-25; s=vt; t мотоциклиста=2 целых 15/60=2,25;
Скорость мотоциклиста=70-20=50
приравниваем 5x=7(x-20) отсюда x=70( скорость автомобилиста).