
для удобства сделаем замену:
![sinx=a,\ a \in [-1;1]](/tpl/images/1003/8025/59535.png)
также:
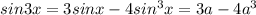
получим:
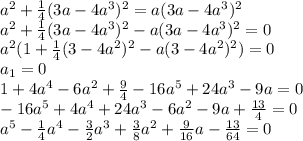
подбираем корни:
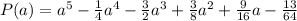
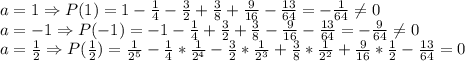

используем схему горнера:(см. вложение)
Получим:
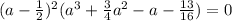
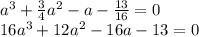
Используем формулу Кардано:
уравнение вида
ax^3+bx^2+cx+d=0
с замены

приводим к виду

где:
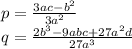
Для данного уравнения(для удобства a заменим на x):

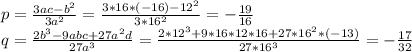
Определим величину Q:
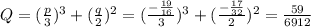
Q>0 => уравнение имеет один действительный и два комплексно-сопряженных корня
Ищем только действительный корень:
![y=\sqrt[3]{-\frac{q}{2}+\sqrt{Q}}+\sqrt[3]{-\frac{q}{2}-\sqrt{Q}}=\sqrt[3]{-\frac{17}{64}+\sqrt{\frac{59}{6912}}}+\sqrt[3]{-\frac{17}{64}-\sqrt{\frac{59}{6912}}}](/tpl/images/1003/8025/5135d.png)
![x=\sqrt[3]{-\frac{17}{64}+\sqrt{\frac{59}{6912}}}+\sqrt[3]{-\frac{17}{64}-\sqrt{\frac{59}{6912}}}-\frac{1}{4}](/tpl/images/1003/8025/931c8.png)
В итоге:
![a_3=\sqrt[3]{\frac{17}{64}+\sqrt{\frac{59}{6912}}}+\sqrt[3]{\frac{17}{64}-\sqrt{\frac{59}{6912}}}-\frac{1}{4}\approx1,0175\notin [-1;1]](/tpl/images/1003/8025/f7d75.png)
обратная замена:
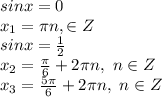
ответ: 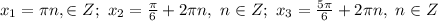

В левой части уравнения применим неравенство Коши
Поэтому это равенство возможно, когда