Пошаговое объяснение:
1)Решите графически систему уравнений.Выполните проверку,подставив найденные решения в уравнения системы :
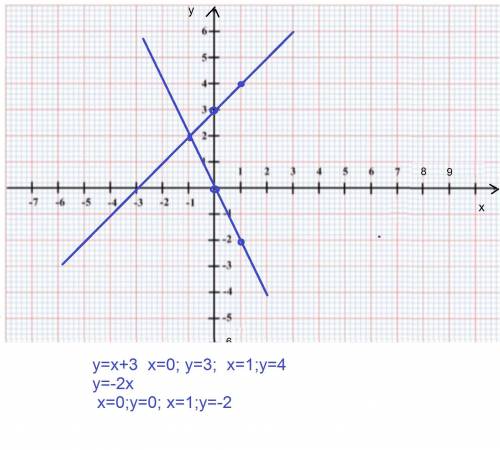
графиком линейных функций являются прямые линии их можно построить по двум точкам
у=х+3 х=0; y=3; x=1;y=4
у=-2х x=0;y=0; x=1;y=-2
графики пересекаются в точке (-1;2)
проверка
-1+3=2
-1*(-2)=2 верно
2)Решите систему подстановки:
у=3-х
4х-у=12 4х-(3-х)=12; 4x-3+x=12; 5x=15; x=3; y=3-3=0; y=0
3) Не выполняя построений,найдите координаты точки пересечения графиков уравнений:
2х+3у=0
х-2у=28 умножим на -2
2х+3у=0
-2х+4у=56 сложим оба уравнения
7у=56; y=8; подставим в первое уравнение 2х+24=0 ;x=-12
(-12;8)
№1.
Подставляем данные координаты в уравнение:
(7;1)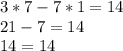
(8;2)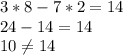
(-7;-5)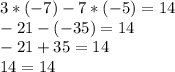
(10;3)
ответ: решениями уравнений являются пары (7;1) и (-7;-5)
№2.
В данном случае систему будем решать методом подстановки. Для этого выразим х из первого уравнения:
Подставляем выраженный х во второе уравнение:
Мы получили уравнение с одной переменной. Решим его, применяя стандартные правила решения уравнений с одной переменной:
Подставляем значение у в первое уравнение:
ответ: (3;-4)
№3.
Так как число дано двузначное, то 15 состоит из двух слагаемых-цифр.
Отсюда: x<10; y<10. (x и y - цифры единиц и десятков искомого числа).
При таком условии 15 можно разбить четырьмя
1) 15=9+6 (число - 96)
2) 15=6+9 (число 69)
3) 15= 8+7 (число 87)
4) 15=7+8 (число 78).
Теперь необходимо выбрать одну из двух пар чисел: 9 и 6, или 8 и 7 ?
Для этого нужно вспомнить, что искомое число на 9 больше числа, в котором поменяли цифры местами, и проверить уравнением каждую пару.
96-69=9
27≠9, следовательно данная пара цифр нам не подходит.
87-78=9
9=9 - эта пара подходит.
Так как нас спрашивали о большем числе, то ответом будет число 87.
ответ: 87.