Следим за последовательностью
60:1=60 -первый ящик
60: 2=30 -во втором
60: 3=20 -в третьем
60: 4=15 -в четвёртом
60 :5=12 - в пятом
60 :6= 10 в шестом
1. A = {x| x∈N, (x+1)² < 27}
т.к. x - натуральное число, то x≥1, то x+1≥2>0,
(x+1)²< 27
5²=25<27 < 36 = 6²
т.к. x - натуральное, то имеем
0<x+1≤5,
1≤x≤4;
A = {1; 2; 3;4},
|A| = 4;
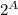 = {∅, {1}, {2}, {3}, {4}, {1; 2}, {1; 3}, {1; 4}, {2; 3}, {2; 4}, {3; 4}, {1; 2; 3},
= {∅, {1}, {2}, {3}, {4}, {1; 2}, {1; 3}, {1; 4}, {2; 3}, {2; 4}, {3; 4}, {1; 2; 3},
{1; 2; 4}, { 1; 3; 4}, {2; 3; 4}, {1; 2; 3; 4}}
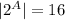
2. A = {0; 1; {2;3}}
B = {1; 2; 3}
C = {5; 6}
C-A = C\A = {5; 6},
A∩C = ∅,
B+C = BΔC = {1; 2; 3; 5; 6},
A - (B∪C) = A\(B∪C) = {0; 1; {2;3}}\{1; 2; 3; 5; 6} = {0; {2; 3}}.
3.
(A∩B)+(A∩C) = (A∩B)Δ(A∩C)

Пошаговое объяснение:
Известно, что в 1 – 60 камешков, 2 – 30, 3 – 20, 4 – 15 Сразу же в глаза бросается, то, что от числа 60, мы делим на нужное нам количество, таким образом:
1. 60:5 = 12 – камешков в 5 ящике;
Делим на 5 из-за того, что нам нужно найти кол-во в 5 ящике.
2. 60:6 = 10 – камешков в 6 ящике;
Делим на 6 из-за того, что нам нужно найти кол-во в 6 ящике.