ответ: 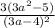
Пошаговое объяснение: Выделяем множитель 3 из 9a^2-15.
Выделяем множитель 3 из 9a^2.
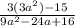
Выделяем множитель 3 из -15.
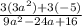
Выделяем множитель 3 из 3(3a^2)+3(-5).
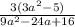
Разложим на множители методом выделения полного квадрата.
Записываем 9a^2 как (3a)^2.
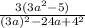
Записываем 16 как 4^2.
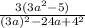
Проверим средний член, перемножив 2ab и сравнивая результат со средним членом исходного выражения.
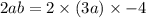
Упростим.
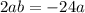
Разложим на множители методом выделения полного квадрата 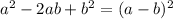 , где a=3a и b=-4.
, где a=3a и b=-4.
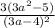
Дано: точка A(3;0), прямая x =12 и число e = 1/2.
Необходимо составить уравнение геометрического места точек, отношения расстояний которых к данной точке A(xA,yA) и к данной прямой x = d равняется е=1/2.
На основании условий задания составим уравнения, выражающие заданные расстояния.
Пусть произвольная точка М(х; у) принадлежит искомой кривой.
Тогда МА =√((3 - x)² + y²).
d(M_d) = 12 - x.
Приравняем эти выражения в заданном соотношении.
2*√((3 - x)² + y²) = 12 - x. Возведём в квадрат обе части.
4(9 - 6x + x² + y²) = 144 - 24x + x²,
36 - 24x + 4x² + 4y² = 144 - 24x + x²,
3x² + 4y² = 108, разделим обе части на 108.
(3x²/108) + (4y²/108) = 1,
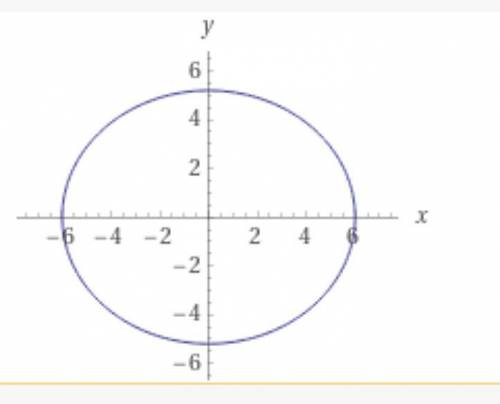
(x²/36) + (y²/27) = 1. Получили уравнение эллипса.
(x²/6²) + (y²/(3√3²) = 1.
График и параметры даны во вложении.

ответ на фото.........