Пошаговое объяснение:
![\tt\displaystyle \[4\frac{5}{{16}}-1\frac{3}{8}=4\frac{5}{{16}}-1\frac{6}{{16}}=3\frac{{21}}{{16}}-1\frac{6}{{16}}=\boxed{2\frac{{15}}{{16}}}\]](/tpl/images/1010/3709/f5eb0.png)
L1: y = -x-4
L2: y = x-6
Пошаговое объяснение:
Дано:
M(1;-5)
L: 3x+3y+2 = 0
Найти: L1, L2
Решение: 1) Для начала выразим прямую L как каноническое уравнение прямой y = kx+b
3x+3y+2 = 0;
3y = -3x-2|:3;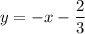
2) Прямые параллельны когда у них меняется свободный член, т.е. k остаётся неизменным, а b нет. Получается коэффициент k у параллельной прямой будет также равен -1
Подставим координаты точки М в каноническое уравнение прямой
-5 = -1*1+b
b = -5+1
b = -4
Уравнение параллельной 3x+3y+2 = 0 прямой, проходящей через точку M(1;-5) будет выглядеть как y = -x-4
3) Для перпендикулярной y = kx+b прямой, проходящей через точку N(x₁,y₁) есть следующая формула:
y-y₁ = -(x-x₁)/k
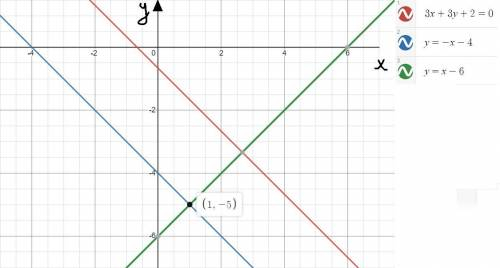
Получается, перпендикулярная y = -x-²/₃ прямая, проходящая через M(1;-5) будет выглядеть как: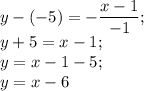
Если построить все данные в одной плоскости, то можно убедиться в правильном нахождении неизвестных прямых(см. вложение)
маленьких квадратов 5*4=20
квадрат в середине, квадрат большой -2
Это было легко. Далее сложнее.
Берем левый верхний квадрат и правее его. Получаем маленький прямоугольничек. Таких сверху будет 6-1=5 и таких прямоугольников 2*1 еще 3 стороны (лево, ...). 5*4=20
Следующим этапом 1*3 - их 6-2=4 сверху. Всего - 4*4=16
1*4 - 6-3=3 3*4=12
1*5 6-4=2 2*4=8
1*6 - один и их 1*4=4
Думаете это все? Нет.
Прибавляем к внутреннему квадрату 4 верхних маленьких, потом левых и т.д. - +4
Теперь прибавляем не только верх, но и низ, а потом лево, право - +2
Но и это еще не все. Берем большой квадрат и отнимаем от него полоску сверху, потом слева,... +4
Теперь прибавляем к внутреннему квадрату 2 стороны верх и право, затем право и низ,... +4
Теперь вроде все.
Итого
20+2+20+16+12+8+4+4+2+4+4=96
Вроде ничего не упустил.
Пошаговое объяснение:
4 5/16 - 1 3/8 = 69/16 - 11/8=47/16=2 15/16 = 2,9375
удачи))