2. 
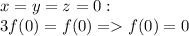
Введем функцию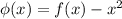 
Тогда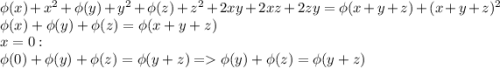 
Т.е.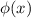 
удовлетворяет функциональному уравнению Коши. А значит 
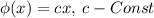(в классе непрерывных функций других решений нет).
Тогда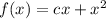 
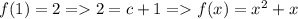
3. Если в область определения входит 0, то
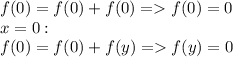
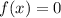- единственное решение.
Пусть функция не определена в 0.
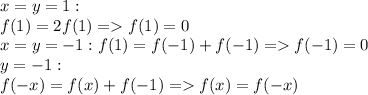
Тогда для удобства ограничим область определения функции положительными числами (а при отрицательном значении аргумента функция примет модуль числа)
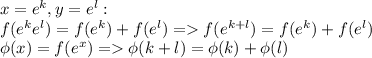
Т.е. 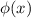удовлетворяет функциональному уравнению Коши. А значит 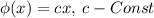(в классе непрерывных функций других решений нет).
![f(e^x)=cx=[x=lnt]=f(t)=c\cdot lnt](/tpl/images/1056/8113/e7416.png)
Вернем исходную область определения функции, заменив переменную на ее модуль: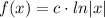 
4. Очевидно, что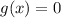 
- одно из решений.
Пусть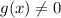 
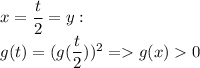
Значит можно логарифмировать
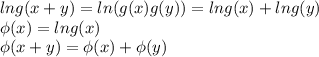
Т.е. 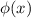удовлетворяет функциональному уравнению Коши. А значит 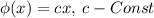(в классе непрерывных функций других решений нет).
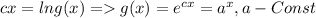
Пошаговое объяснение:
Из уравнения
следует, что среди чисел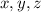
либо все нечетные, либо одно.
Заметим, что
Из нашего условия это преобразуется как
Но мы знаем, что среди чисел
либо все четные, либо одно. Если четны все, то они могут быть равны только 
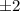в этом случае числа 
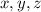могут быть равны с точностью до перестановки только 
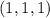или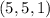 
. Второе решение не подходит в исходное уравнение, поэтому его отметаем. Если же среди чисел 
только одно четное, то оно обязано быть равно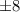 
, а остальные - 
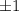. В этом случае 
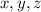равны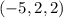 
, 
, 
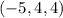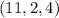. Из этих троек нам подходит только вторая.
В итоге, решений всего два.