Даны точки P(-1,2,1); Q(3 ,-4 , 2) и плоскость 2x + 4y - 3z + 5=0.
Находим координаты вектора m, проходящего через точки P и Q.
m = (3-(-1)=4; -4-2=-6; 2-1=1) = (4; -6; 1).
Второй вектор - это нормальный вектор заданной плоскости. Он будет лежать в искомой плоскости. Его координаты берём из уравнения:
n = (2; 4; -3).
Теперь берём точку P(-1,2,1) и 2 вектора, которые будут лежать в искомой плоскости: m = (4; -6; 1) и n = (2; 4; -3).
Плоскость, проходящая через точку М0(х0;у0;z0) и параллельная данным (непараллельным между собой) прямым K1 и K2 (или векторам a1 и а2), представляется уравнением:
x-x0 y-y0 z-z0
nx ny nz
mx my mz = 0.
Подставляем данные:
x+1 y-2 z-1
2 4 -3
4 -6 1 = 0.
Решив эту матрицу, получаем -14x - 14y - 14z + 42 = 0.
Сократив на -14, получаем уравнение искомой плоскости:
x + y + z - 3 = 0.
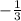
Пошаговое объяснение:
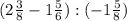
Переведем в неправильную дробь: (Умножаем целое число на знаменатель и прибавляем к числителю.)
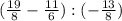
Для сложения либо вычитания дробей нужно привести их к общему знаменателю, для этого нужно:
Найти наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель). В нашем случае это 24 Разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель. У нас: 24/8=3 24/6=4 Умножить числитель и знаменатели каждой дроби на ее дополнительный множитель. Получается 8 и 19 на 3, 6 и 11 на 4.После умножения получается так:

Теперь нужно вычесть дробь из дроби, для этого нужно найти разность числителей, а знаменатели не трогать, получается 57-44=13 :
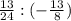
При делении дробь на дробь нужно вторую дробь перевернуть, если можно сократить и выполнить умножение:
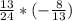
Сразу видим 13 сверху и снизу, их можно сократить и они будут равны единице. Также видим 8 и 24, сокращаем, получается 1 сверху и 3 снизу. Получается:
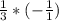
Остается закончить умножение, для этого нужно умножить числитель на числитель, знаменатель на знаменатель и получится:
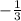
=============================
Пошаговое объяснение: