15 целых чисел расположено на координатной прямой между числами (-9) и 7
Пошаговое объяснение:
Числа, расположенные между числами (-9) и 7:
-8, -7, -6, -5, -4, -3, -2, -1, 0, 1. 2, 3, 4, 5, 6 - 15 целых чисел
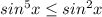
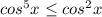
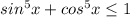 справедливое при всех x∈R причем равенство будет верным когда
справедливое при всех x∈R причем равенство будет верным когда 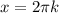
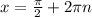
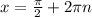 и
и 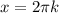 где k,n∈Z
где k,n∈Z
15
-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6