9.999.999
Вот так вот
Если не сложно поставь лучшее решение...))
№1 1) х*4=350-70
4х=280
х= 280/4
х=70
Проверка: 70*4=350-70
280=280
ответ: х=70
2) 750/х=32+18
750/х=50
х=750/50
х=15
Проверка: 750/15=32+18
50=50
№2 387 /50
-350 7 (ост.37)
37
5893 /70
-5880 84 (ост. 13)
13
764 /200
-600 3 (ост. 164)
164
9361 /600
- 9000 15 (ост.361)
361
А проверить их можно так:
1) 50*7= 350+37=387
2)70*84=5880+13=5893
3)200*3=600+164=764
4)600*15=9000+361=9361
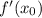
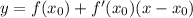

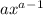 - где а- степень
- где а- степень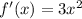 - вот такая вот производная
- вот такая вот производная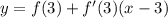
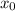 :
: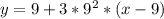
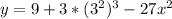
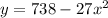
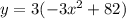 - это и есть касательная в ДАННОЙ точке.
- это и есть касательная в ДАННОЙ точке.
Для этого можно взять какое нибудь число и умножить его на 99, к примеру, возьмём 71241 и умножим на 99, получим семь знаков:
7052859 (число кратное 99, то есть делится на 99)