Пошаговое объяснение:
Диагональ прямоугольника равна по теореме Пифагора :
sqrt ( 6^2+ 8^2) =10( см). В прямоугольном треугольнике с высотой пирамиды гипотенуза равна 13 см, один из катетов - 5см ( половина диагонали прямоугольника). Высота по теореме Пифагора равна sqrt(13^2 - 5^2)=12(см). Площадь полной поверхности складывается из площади основания, площадей двух пар равных боковых граней. Площадь основания равна 6х8=48 (кв. см). Апофемы ( высоты боковых граней ) находятся из прямоугольных треугольников с высотами пирамиды. Вторые катеты равны половине сторон основания. Т.о. одна апофема по теореме Пифагора равна sqrt (12^2 + 4^2)=4 sqrt 10. Другая апофема равна sqrt(12^2 +3^2)=sqrt 153. Площадь боковой грани с первой апофемой равна 6х4sqrt 10/2=12 sqrt 10. Площадь боковой грани со второй апофемой равна 8хsqrt 153 /2= 4 sqrt 153. И площадь полной поверхности пирамиды равна ( 48 + 24 sqrt 10+ 8 sqrt 153) кв. см.
2 задача. 2 боковые ребра находятся из прямоугольных треугольников, содержащих высоту пирамиды, а второй катет - половина известной диагонали (6:2=3). Мы получаем египетский треугольник : катеты равны 4 см и 3 см , поэтому боковое ребро = 5 см. Чтобы найти оставшиеся боковые рёбра, надо
ответ: a∈(-1;-2/3) ∪ (-2/3 ; -1/3)
Пошаговое объяснение:
ОДЗ: 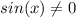
Используем формулу:
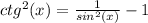
Замена: 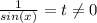
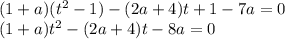
Заметим, что для того чтобы существовало одно решение на интервале (0;π/2), необходимо и достаточно, чтобы выполнялось условие 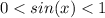 , в этом случае на промежутке (0;π/2) будет существовать ровно ОДНО значение x, в противном случае, решений на данном промежутке не будет.
, в этом случае на промежутке (0;π/2) будет существовать ровно ОДНО значение x, в противном случае, решений на данном промежутке не будет.
Откуда, должно выполнятся условие: 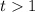
По условию, нужно найти те значения параметра a, при которых будет более одного решения на интервале (0;π/2), а значит данное уравнение должно иметь как минимум два положительных решения.
1)
Рассмотрим линейный случай, ибо может быть бесконечное число решений: 
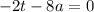 - одно решение
- одно решение
2) Основной случай.
Должно быть два корня, каждый из которых больше единицы :
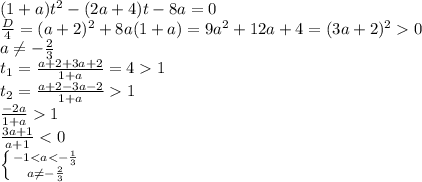
a∈(-1;-2/3) ∪ (-2/3 ; -1/3)
р1= вероятность попал первое орудие
р2= вероятность попал второе орудие
р1=?
р2=0,8
Всего возможных вариантов 4.
1 Попал ; 2 не попал;
p1•(1-р2)= р1•(1-0,8)= р1• 0,2
1 попал ; 2 попал;
р1•р2= р1•0,8
1 не попал; 2 попал
(1-р1)• р2= (1-р1)•0,8
1 не попал; 2 не попал
(1-р1)• (1-р2) = (1-р1)• (1-0,8)= (1-р1)•0,2
По условию вероятность 0,38 при попадании одном из двух
или первым орудием попал
1 Попал ; 2 не попал;
p1•(1-р2)= р1•(1-0,8)= р1• 0,2
Или вторым орудием попал;
1 не попал; 2 попал ;
(1-р1)• р2= (1-р1)•0,8
вероятность равна сумме их вероятностей и по условию =0,38
р1•0,2+ (1-р1)•0,8= 0,38
0,2•р1+ 0,8- 0,8•р1 = 0,38
0,8-0,38= 0,8•р1-0,2•р1
0,42=0,6•р1
р1=0,42 : 0,6
р1= 0,7
ответ: вероятность 0,7 поражения цели при одном выстреле первым орудием
5.если разместить точку В в любое место отрезка ОА, то вероятность, что отрезок ОА меньше L/2 зависит от положения точки В искомая вероятность равна отношению площади заштрихованной фигуры к площади прямоугольника со сторонами L x 1
площадь заштрихованной фигуры = L * 1/2 +L * 1/2*1/2 = L*3/4
площади прямоугольника = L*1
искомая вероятность равна = 3/4
Пошаговое объяснение: