7. 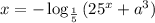
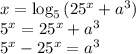
Пусть 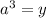 , количество корней от этого не изменится.
, количество корней от этого не изменится.
Рассмотрим функцию 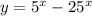 :
:
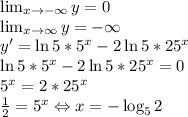
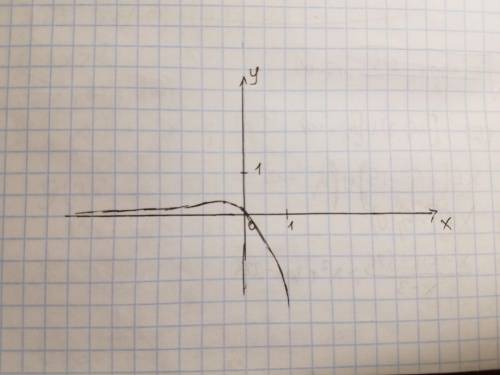
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно 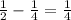 . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
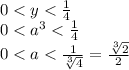
ответ: ![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
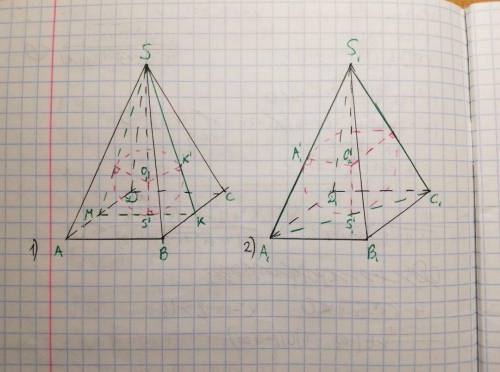
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
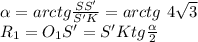
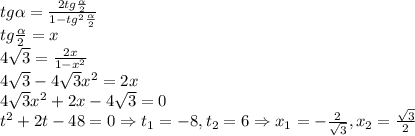
Учитывая, что угол находится в первой четверти, 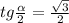
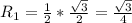
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
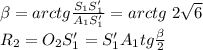
Решая аналогичное уравнение, получаем 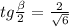
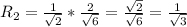
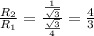
ответ: 4 : 3
4929
Пошаговое объяснение:
Разобьём область 162*117 на 3 области A, B, C с размерами 160*116, 2*116 и 1*162.
Область A можно разбить на (160/4)*(116/4)=40*29=1160 блоков 4*4.
Область B можно разбить на (2/2)*(116/2)=58 блоков 2*2.
Область C можно разбить на (1/1)*(162/1)=162 блоков 1*1.
В сумме имеется 1160+58+162=1380 блоков. Посмотрим, что будет, если попытаться разбить большие блоки на более мелкие.
1) Если разбить блок 4*4 на 4 блока 2*2, то уйдет 1 блок 4*4, добавятся 4 блока 2*2, то есть суммарное количество блоков увеличится на 3.
2) Если разбить блок 2*2 на 4 блока 1*1, то суммарное число блоков также увеличится на 3.
(Аналогично, если пытаться объединять блоки 1*1 в блоки 2*2 или 2*2 в 4*4, то суммарное число блоков будет изменяться на величину, кратную 3).
Таким образом, вне зависимости от разбиения на блоки остаток от деления на 3 количества блоков будет одинаковым. Для прямоугольника 162*117 он равен 0. Поэтому минимальным N может быть число, кратное 3, то есть 4929.
Как этого добиться?
1) Сначала разобьем 236 блоков 4*4 на блоки 1*1, тем самым добавив к суммарному числу блоков (16-1)*236=3540. Блоков стало 4920
2) Разобьем 3 блока 2*2 на блоки 1*1. Добавится (4-1)*3=9 блоков. Теперь блоков 4929.