Как применять здесь признак Дирихле, я не придумал. Хорошо, что автор задания не разрешил пользоваться им)). А может быть автор имеет в виду, что нельзя использовать знание, при каких значениях параметра ряд Дирихле сходится, а при каких расходится? Ну не будем, так и быть. Но если ряд Дирихле случайно появится, мы не виноваты, и даже будем делать вид, что не узнали его.
Воспользуемся признаком сравнения:
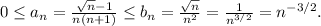
Докажем, что ряд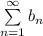 
сходится. Докажем это с интегрального признака Коши. Монотонное убывание функции
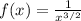при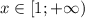 
очевидно (если не верите - посчитайте производную). Обычно требуют сделать проверку стремления f(x) к нулю на плюс бесконечности, но на самом деле признак работает и без этого условия (другое дело, если функция не стремится к нулю, расходимость ряда очевидна и без всякого признака). Но если Вас это напрягает - посмотрите на функцию и у Вас не будет никаких сомнений в стремлении ее к нулю. Остается исследовать несобственный интеграл
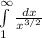на сходимость.
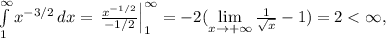
то есть интеграл сходится, а тогда и ряд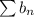 
(неужели это ряд Дирихле? вот сюрприз!) сходится, а тогда и ряд 
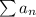сходится по признаку сравнения.
45
Пошаговое объяснение:
Для начала рассмотрим треугольник ADC, который лежит в основании.
Угол d равен 90 градусам, то есть за т. Пифагора, можем найти AC
AC=корень из (2^2+(корень из 5)^2)=корень из 9= 3.
С треугольника A1CA, найдем угол C. tgC=AA1:AC=3/3=1. То есть угол C=45 градусам...