Question

Вася, изучая компьютерную программу, развлекался, поворачивая равносторонний треугольник относительно его центра по часовой стрелке: сначала на 1/9 градуса, затем второй треугольник на 1/3 градуса, затем третий треугольник на 1 градус и т.д. до 3(в сотой степени) градусов, увеличивая на каждом шаге угол поворота в три раза. сколько всего разных положений треугольника мог получить вася, включая начальное? ​

Answer 1

7

Пошаговое объяснение:

Окружность можно разбить на секторы с градусной мерой 1/9 градуса, так как все повороты треугольника происходят на угол, кратный 1/9 градуса. Пусть 1 деление соответствует 1/9 градуса. Тогда происходили такие действия:

1) Треугольник повернули на 1 деление - соответствует углу 1/9 градуса

2) Повернули на 3 деления - соответствует углу 1/3 градуса

3) Повернули на 9 делений - соответствует 1 градусу

...

103) Повернули на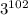  $3^{102}$ деления - соответствует  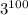$3^{100}$ градусов.

Тогда для поворота номер n величина поворота относительно начального положения треугольника (в делениях) равна сумме геометрической прогрессии: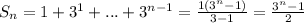 $S_n=1+3^1+...+3^{n-1}=\frac{1(3^n-1)}{3-1}=\frac{3^n-1}{2}$

Можно заметить, что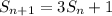 $S_{n+1}=3S_n+1$. Действительно, $3*S_n+1=3*\frac{3^n-1}{2}+1=\frac{3^{n+1}-3}{2}+1=\frac{3^{n+1}-1}{2}=S_{n+1}$.

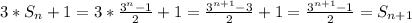Видим, что два положения треугольника совпадают, если разность углов поворота кратна 120 градусам или же 120/(1/9)=1080 делений, так как треугольник равносторонний.

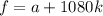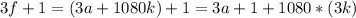Пусть был угол поворота в делениях $f=a+1080k$, где $0\le a$. При новом повороте треугольника угол поворота станет равным $3f+1=(3a+1080k)+1=3a+1+1080*(3k)$. Это значит, что преобразование f -> 3f+1 можно применять с отсечением периода.

Задача свелась к тому, чтобы найти количество уникальных значений последовательности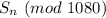 $S_n\ (mod\ 1080)$.

Тогда построим последовательность положений треугольника:

0) 0 (начальное положение)

1) 3*0+1 (mod 1080) = 1

2) 1*3+1 (mod 1080) = 4

3) 4*3+1 (mod 1080) = 13

4) 13*3+1 (mod 1080) = 40

5) 40*3+1 (mod 1080) = 121

6) 121*3+1 (mod 1080) = 364

7) 364*3+1 (mod 1080) = 13

Видим, что на шаге 7 появилось уже полученное ранее значение. Следовательно, дальше повороты будут получаться так же циклически. Поэтому количество уникальных положений треугольника равно 7.