Достаточно найти точки х на которых
(х+1)^2*(5-x) принимает наибольшее и наименьшее значения .
Дифференцируем.
2(х+1)*(5-х)-(х+1)^2
Нули этой функции те же, что и у
2(х+1)*(5-х)-(х+1)^2=(х+1)*(10-2х-х-1)=-(х+1)(9-3х)
Производная равна 0 в точках х=-1 и х=3
Значит локальные экстремумы (или точки перегиба) находятся в этих точках.
В пределах отрезка два возможных экстремума в точке х=-1 и х=3.
Конечно, можно убедиться, что в этих точках производная меняет знак, поэтому это экстремумы.
Однако, достаточно посчитать значения функции в этих точках и на краях отрезка :
у(-3)=(2*4*8)^(1/3)-2=2
y(-1)=-2
y(3)=(2*16*2)^(1/3-2=2
Итак функция принимает два равных максимальных значения при х=3 и х=-3 и минимальное значение при х=-1.
Максимальные значения равны 2. Минимальное значение равно -2.
Здесь ^ -возведение в степень.
Найдем сначала наибольшее и наименьшее значения функции
y=(x+1)²(5-x). В силу того, что функция извлечения корня третьей степени монотонно возрастает, достаточно будет затем умножить найденные значения на 2, извлечь корень третьей степени из получившихся чисел, после чего вычесть из них 2.
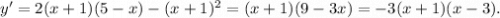
Внутри интервала (-3;3) лежит один из нулей производной - это x=-1. Найдем значения функции в точках -3; 3 (концах отрезка) и в точке -1:
y(-3)=y(3)=32 - наибольшее значение; y(-1)=0 - наименьшее значение.
Осталось с получившимися числами проделать указанные операции - умножить на 2, извлечь корень третьей степени и вычесть 2:
![\sqrt[3]{2\cdot 32}-2=4-2=2;\ \sqrt[3]{2\cdot 0}-2=-2.](/tpl/images/2074/3094/1128c.png)
ответ: наибольшее значение равно 2 и достигается на концах отрезка, наименьшее значение равно минус 2 и достигается в точке минус 1.
возможно x принимает любое значение
Пошаговое объяснение:
sinx область определения является множество всех чисел
область определения постоянной функций(5) также как и синус множество всех чисел
то есть их пересечения x€R