15 правдивых
Пошаговое объяснение:
Все нечётные жрецы, кроме первого, будут говорить правду.
Перед любым нечётным числом количество чётных чисел равно количеству нечётных и их разность равна нулю: x-x=0;
Первый жрец обязан солгать, так как до него никто не говорил и второй тоже солжёт, так как до него говорил только один.
прибавляем первого жреца к чётным жрецам (которые лгут) и получаем, что перед любым следующим нечётным жрецом лгунов было на (x+1)-(x-1)=2 человека больше. Значит все нечётные жрецы, кроме первого, должны говорить правду.
Получается, что из 31 жреца 16 лжецов и 15 правдивых.
3) При возведении обеих частей уравнения в одинаковую четную степень не всегда получаются равносильные уравнения.
Пошаговое объяснение:
1) Утверждение не верно.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня. Например:
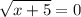
Это уравнение имеет корень х = -5!
2) Утверждение не верно.
Например, если возвести в нулевой степень (0 принадлежит множеству действительных чисел) уравнение, имеющий только корень х=0:
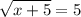
то получим
1 ≡ 1, что означает, последнее верно для любого х∈R.
3) Утверждение верно.
Уравнения называются равносильными, если имеют одно и то же множество корней.
В самом деле, рассмотрим иррациональное уравнение, которое не имеет корней:
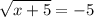
После возведения в квадрат получим:
x+5=25
А это уравнение имеет корень x=20!
14-72:(d-3)=8
72:(d-3)=14-8
72:(d-3)= 6
d-3=72:6
d-3= 12
d=12+3
d=15
проверка
14-72:(15-3)=8
14-72:12=8
14- 6=8
8=8
(r:16)*13+11=50
(r:16)*13=50-11
(r:16)*13= 39
r:16=39:13
r:16=3
r=16*3
r= 48
проверка
(48:16)*13+11=50
3*13+11=50
39+11=50
50=50
(980:n)*18-84=276
(980 :n)*18=276+84
(980:n)*18= 360
980:n=360:18
980:n= 20
n=980:20
n= 49
проверка
(980:49)*18-84=276
20*18-84=276
360-84=276
276=276
96+(80-х):14=100
(80-х):14=100-96
(80-х):14= 4
80-х=14*4
80-х= 56
х=80-56
х= 24
проверка
96+(80-24):14=100
96+ 56:14=100
96+ 4=100
100=100